Question

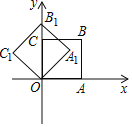
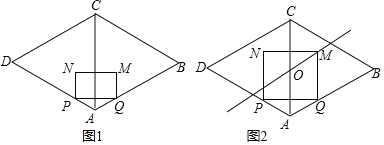
【题目】如图①,在菱形中, ，.点从点出发以每秒2个单位的速度沿边向终点运动，过点作交边于点，过点向上作，且，以、为边作矩形.设点的运动时间为（秒），矩形与菱形重叠部分图形的面积为.

（1）用含的代数式表示线段的长.

（2）当点落在边上时，求的值.

（3）当时，求与之间的函数关系式，

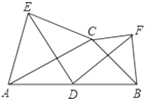
（4）如图②,若点是的中点，作直线.当直线将矩形分成两部分图形的面积比为时，直接写出的值

Answer 1

【答案】（1）；（2） ；（3） ；（4） 或 ．

【解析】

（1）由菱形性质得∠D=∠B=60°，AD=AB=CD=4，△ACD是等边三角形，证出△APQ是等腰三角形，得出PF=QF，PF=PAsin60°=t，即可得出结果；

（2）当点M落在边BC上时，由题意得：△PDN是等边三角形，得出PD=PN，由已知得PN=PQ=3t，得出PD=3t，由题意得出方程，解方程即可；

（3）当0＜t≤时，PQ=2t，PN=PQ=3t，S=矩形PQMN的面积=PQ×PN，即可得出结果；当＜t＜1时，△PDN是等边三角形，得出PE=PD=AD-PA=4-2t，∠FEN=∠PED=60°，得出NE=PN-PE=5t-4，FN=NE=（5t-4），S=矩形PQMN的面积-2△EFN的面积，即可得出结果；

（4）分两种情况：当0＜t≤时，△ACD是等边三角形，AC=AD=4，得出OA=2，OG是△MNH的中位线，得出OG=4t-2，NH=2OG=8t-4，由面积关系得出方程，解方程即可；

当＜t≤2时，由平行线得出△OEF∽△MEQ，得出，即，解得EF=，得出EQ=，由三角形面积关系得出方程，解方程即可．

（1）∵在菱形ABCD中，∠B=60°，

∴∠D=∠B=60°，AD=AB=CD=4，△ACD是等边三角形，

∴∠CAD=60°，

∵PQ⊥AC，

∴△APQ是等腰三角形，

∴PF=QF，PF=PAsin60°=2t×=t，

∴PQ=2t；

（2）当点M落在边BC上时，如图2所示：

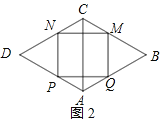
由题意得：△PDN是等边三角形，

∴PD=PN，

∵PN=PQ=×2t=3t，

∴PD=3t，

∵PA+PD=AD，

即2t+3t=4，

解得：t=．

（3）当0＜t≤时，如图1所示：

PQ=2t，PN=PQ=×2t=3t，

S=矩形PQMN的面积=PQ×PN=2t×3t=6t2；

当＜t＜1时，如图3所示：

∵△PDN是等边三角形，

∴PE=PD=AD-PA=4-2t，∠FEN=∠PED=60°，

∴NE=PN-PE=3t-（4-2t）=5t-4，

∴FN=NE=（5t-4），

∴S=矩形PQMN的面积-2△EFN的面积=6t2-2××（5t-4）2=-19t2+40t-16，

即S=-19t2+40t-16；

（4）分两种情况：当0＜t≤时，如图4所示：

∵△ACD是等边三角形，

∴AC=AD=4，

∵O是AC的中点，

∴OA=2，OG是△MNH的中位线，

∴OG=3t-（2-t）=4t-2，NH=2OG=8t-4，

∴△MNH的面积=MN×NH=×2t×（8t-4）=×6t2，

解得：t=；

当＜t≤2时，如图5所示：

∵AC∥QM，

∴△OEF∽△MEQ，

∴，即，

解得：EF=，

∴EQ=，

∴△MEQ的面积=×3t×（）=×6t2，

解得：t=；

综上所述，当直线OM将矩形PQMN分成两部分图形的面积比为1：2时，t的值为或．