题目内容
【题目】定义：有一组对边相等而另一组对边不相等的凸四边形叫做“等对边四边形”．
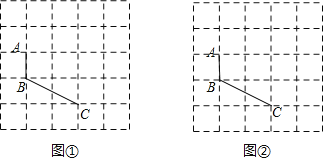
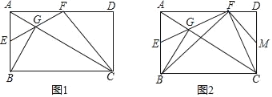
(1)已知：图①、图②是5×5的正方形网格，线段AB、BC的端点均在格点上．在图①、图②中，按要求以AB、BC为边各画一个等对边四边形ABCD．
要求：四边形ABCD的顶点D在格点上，且两个四边形不全等．
(2)若每个小正方形网格的边长为一个单位，请直接写出(1)问中所画每个等对边四边形ABCD的面积______．
【答案】(1)见解析；(2)4.
【解析】
(1)根据“等对边四边形”的定义画出图形即可．
(2)分别求出两个四边形的面积即可．
解：(1)满足条件的四边形如图所示．
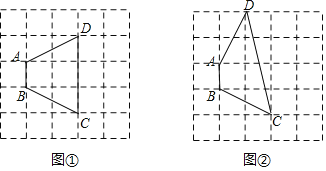
(2)图1中，四边形ABCD的面积=
(1+3)×2=4，
图2中，四边形ABCD的面积=2×4-×1×2-×1×2-×1×4=4．
故四边形ABCD的面积都是4，
故答案为4．
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
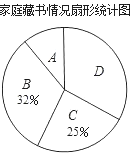
【题目】在“书香校园”活动中，某校为了解学生家庭藏书情况，随机抽取本校部分学生进行调查，并绘制成部分统计图表如下：
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息，解答下列问题：
(1)该调查的样本容量为_____，a＝_____；
(2)在扇形统计图中，“A”对应扇形的圆心角为_____°；
(3)若该校有2000名学生，请估计全校学生中家庭藏书200本以上的人数．
