Question

【题目】已知：如图.D是的边上一点，，交于点M，.

（1）求证：；

（2）若，试判断四边形的形状，并说明理由.

Answer 1

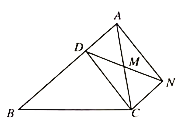
【答案】（1）证明见解析；（2）四边形ADCN是矩形，理由见解析.

【解析】

（1）根据平行得出∠DAM＝∠NCM，根据ASA推出△AMD≌△CMN，得出AD＝CN，推出四边形ADCN是平行四边形即可；

（2）根据∠AMD＝2∠MCD，∠AMD＝∠MCD＋∠MDC求出∠MCD＝∠MDC，推出MD＝MC，求出MD＝MN＝MA＝MC，推出AC＝DN，根据矩形的判定得出即可．

证明：（1）∵CN∥AB，

∴∠DAM＝∠NCM，

∵在△AMD和△CMN中，

∠DAM＝∠NCM

MA＝MC

∠DMA＝∠NMC，

∴△AMD≌△CMN（ASA），

∴AD＝CN，

又∵AD∥CN，

∴四边形ADCN是平行四边形，

∴CD＝AN；

（2）解：四边形ADCN是矩形，

理由如下：∵∠AMD＝2∠MCD，∠AMD＝∠MCD＋∠MDC，

∴∠MCD＝∠MDC，

∴MD＝MC，

由（1）知四边形ADCN是平行四边形，

∴MD＝MN＝MA＝MC，

∴AC＝DN，

∴四边形ADCN是矩形．