Question

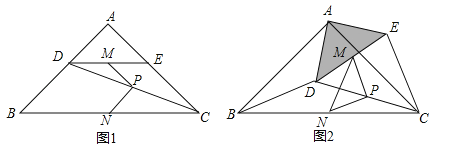
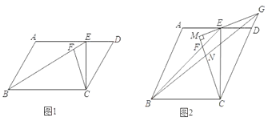
【题目】如图，在平行四边形ABCD中，CE⊥BC交AD于点E，连接BE，点F是BE上一点，连接CF．

（1）如图1，若∠ECD＝30°，BC＝BF＝4，DC＝2，求EF的长；

（2）如图2，若BC＝EC，过点E作EM⊥CF，交CF延长线于点M，延长ME、CD相交于点G，连接BG交CM于点N，若CM＝MG，求证：EG＝2MN．

Answer 1

【答案】（1）EF＝﹣4；（2）证明见解析.

【解析】

（1）利用勾股定理求出EC，BE即可解决问题．

（2）如图2中，延长GM到H，使得MH＝MG，连接CH，BH．想办法证明EG＝BH，BH＝2MN即可解决问题．

（1）解：如图1中，

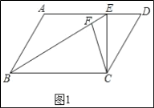
∵四边形ABCD是平行四边形，

∴AD∥BC，

∵EC⊥BC，

∴AD⊥EC，

∴∠BCE＝∠CED＝90°，

∵∠ECD＝30°，CD＝2，

∴CE＝CDcos30°＝，

在Rt△BCE中，BE＝＝，

∵BC＝CF＝4，

∴EF＝BE﹣BF＝-4．

（2）证明：如图2中，延长GM到H，使得MH＝MG，连接CH，BH．

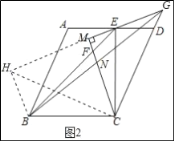
∵CM＝MG＝MH，CM⊥GH，

∴∠HCG＝90°，CH＝CG，

∴∠HCG＝∠BCE，

∴∠BCH＝∠ECG，

∵CB＝CE，

∴△BCH≌△ECG（SAS），

∴BH＝EG，∠CHB＝∠CGE＝45°，

∵∠CHG＝45°，

∴∠BHG＝90°，

∴∠BHG＝∠CMG＝90°，

∴MN∥BH，∵HM＝HG，

∴BN＝NG，

∴BH＝2MN，

∴EG＝2MN．