题目内容
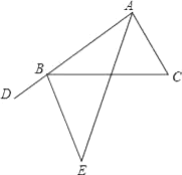
【题目】把两个含有45°角的大小不同的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.求证:AF⊥BE.
【答案】.解:(1)证明:在△ACD和△BCE中,
 AC=BC,
AC=BC,
∠DCA=∠ECB=90°,
DC=EC,
∴△ACD≌△BCE(SAS). 5分
∴∠DAC=∠EBC. 6分
∵ ∠ADC=∠BDF,
∴ ∠EBC+∠BDF=∠DAC+∠ADC=90°.
∴ ∠BFD=90°. 8分
∴AF⊥BE. 9分
【解析】试题根据题意得出∠DEC=∠EDC=45°,∠CBA=∠CAB=45°,则EC=DC,BC=AC,得出△ECD和△BCA为等腰直角三角形,然后证明△BEC和△ADC全等,从而得出∠EBC=∠DAC,根据∠DAC+∠CDA=90°得出
∠BFD=90°,从而得出垂直.
试题解析:AF⊥BE,理由如下:
由题意可知∠DEC=∠EDC=45°,∠CBA=∠CAB=45°, ∴EC=DC,BC=AC,又∠DCE=∠DCA=90°,
∴△ECD和△BCA都是等腰直角三角形, ∴EC=DC,BC=AC,∠ECD=∠ACB=90°.
在△BEC和△ADC中, EC=DC,∠ECB=∠DCA,BC=AC, ∴△BEC≌△ADC(SAS).
∴∠EBC=∠DAC.∵∠DAC+∠CDA=90°,∠FDB=∠CDA,∴∠EBC+∠FDB=90°.
∴∠BFD=90°,即AF⊥BE.

练习册系列答案
相关题目