Question

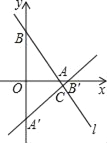
【题目】如图，直线与x轴、y轴分别交于点A，B，另一直线与x轴、y轴分别交于点C，D，两直线相交于点M．

求点M的坐标；

连接AD，求△AMD的面积．

Answer 1

【答案】(1)点M的坐标(1，2)；(2)S△AMD＝2.

【解析】

（1）y=-x+3与y=x+1组成方程组，即可求出M的坐标；

（2）通过一次函数求出A，B，C，D四点的坐标，S△AMD=S△AMC-S△ACD就可求出面积．

(1)由，解得，

故点M的坐标(1，2)；

(2)∵直线y＝﹣x+3与x轴、y轴分别交于点A，B，另一直线y＝x+1与x轴、y轴分别交于点C，D，

∴A(3，0)，B(0，3)，C(-1，0)，D(0，1)，AC＝4，

∴S△AMD＝S△AMC﹣S△ACD＝＝2