题目内容
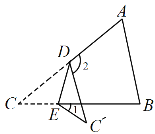
【题目】如图,在△ABC中,∠ACB=45°,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,若∠ACE=20°,则∠B的度数为( )

A. 60°B. 65°C. 70°D. 75°
【答案】B
【解析】
根据已知条件得到△ADC是等腰直角三角形,求得AD=CD,∠CAE=∠ACD=45°,根据全等三角形的性质得到∠B=∠DEC,根据三角形的外角的性质即可得到结论.
解:∵AD⊥BC,∠ACB=45°,
∴△ADC是等腰直角三角形,
∴AD=CD,∠CAE=∠ACD=45°,
在Rt△ABD与Rt△CED中![]() ,
,
∴Rt△ABD≌Rt△CED(HL),
∴∠B=∠DEC,
∵∠DEC=∠CAE+∠ACE=45°+20°=65°,
∴∠B=65°,
故选:B.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目