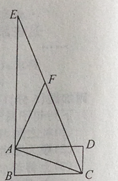题目内容
【题目】在平面直角坐标系xOy中,对“隔离直线”给出如下定义:
点P(x,m)是图形G1上的任意一点,点Q(x,n)是图形G2上的任意一点,若存在直线l:kx+b(k≠0)满足m≤kx+b且n≥kx+b,则称直线l:y=kx+b(k≠0)是图形G1与G2的“隔离直线”.
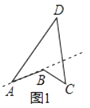
如图1,直线l:y=﹣x﹣4是函数y= ![]() (x<0)的图象与正方形OABC的一条“隔离直线”.
(x<0)的图象与正方形OABC的一条“隔离直线”.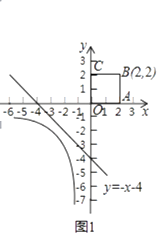
(1)在直线y1=﹣2x,y2=3x+1,y3=﹣x+3中,是图1函数y= ![]() (x<0)的图象与正方形OABC的“隔离直线”的为;
(x<0)的图象与正方形OABC的“隔离直线”的为;
请你再写出一条符合题意的不同的“隔离直线”的表达式:;
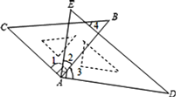
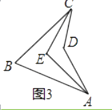
(2)如图2,第一象限的等腰直角三角形EDF的两腰分别与坐标轴平行,直角顶点D的坐标是( ![]() ,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
,1),⊙O的半径为2.是否存在△EDF与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式;若不存在,请说明理由;
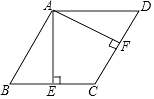
(3)正方形A1B1C1D1的一边在y轴上,其它三边都在y轴的右侧,点M(1,t)是此正方形的中心.若存在直线y=2x+b是函数y=x2﹣2x﹣3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,请直接写出t的取值范围.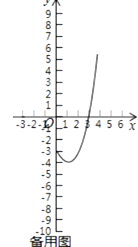
【答案】
(1)y1=﹣2x;y=﹣3x
(2)
连接OD,过点D作DG⊥x轴于点G,如图.
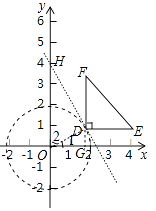
在Rt△DGO中,OD= ![]() =2,
=2,
sin∠1= ![]() =
= ![]() ,
,
∴∠1=30°,∠2=60°,
∵⊙O的半径为2,
∴点D在⊙O上.
过点D作DH⊥OD交y轴于点H,
∴直线DH是⊙O的切线,也是△EDF与⊙O的“隔离直线”.
在Rt△ODH中,OH= ![]() =4,
=4,
∴点H的坐标是(0,4),
∴直线DH的表达式为y=﹣ ![]() x+4,
x+4,
即所求“隔离直线”的表达式为y=﹣ ![]() x+4
x+4
(3)
如图,
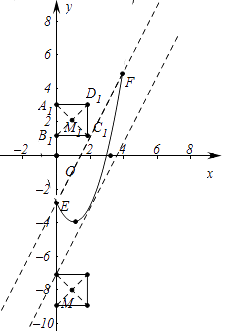
由题意F(4,5),当直线y=2x+b经过点F时,5=8+b,
∴b=﹣3,
∴直线y=2x﹣3,即图中直线EF,
∵正方形A1B1C1D1的中心M(1,t),
易知正方形正方形A1B1C1D1的边长为2,
当x=2时,y=1,
∴C1(2,1),直线EF是函数y=x2﹣2x﹣3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”,此时t=2,
当直线y=2x+b与y=x2﹣2x﹣3只有一个交点时,
![]() 消去y得到x2﹣4x﹣3+b=0,
消去y得到x2﹣4x﹣3+b=0,
由△=0,可得16﹣4(﹣3﹣b)=0,
解得b=﹣7,
此时易知M(1,﹣8),t=﹣8,
根据图象可知,当t≥2或t≤﹣8时,直线y=2x+b是函数y=x2﹣2x﹣3(0≤x≤4)的图象与正方形A1B1C1D1的“隔离直线”
【解析】解:(1)根据的“隔离直线”的定义可知y1=﹣2x,是图1函数y= ![]() (x<0)的图象与正方形OABC的“隔离直线”,直线y=﹣3x也是图1函数y=
(x<0)的图象与正方形OABC的“隔离直线”,直线y=﹣3x也是图1函数y= ![]() (x<0)的图象与正方形OABC的“隔离直线”,所以答案是y1=﹣2x,y=﹣3x.
(x<0)的图象与正方形OABC的“隔离直线”,所以答案是y1=﹣2x,y=﹣3x.

 口算能手系列答案
口算能手系列答案