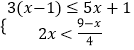题目内容
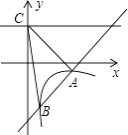
【题目】一副三角板按如图放置，下列结论：①∠1=∠3；②若BC∥AD，则∠4=∠3；③若∠2=15°，必有∠4=2∠D；④若∠2=30°，则有AC∥DE. 其中正确的有_____.
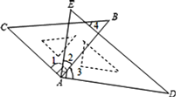
【答案】①③④
【解析】
根据余角的概念和同角的余角相等判断①；根据平行线的性质判断②；根据三角形的外角性质计算判断③；平行线的判定定理判断④．
解：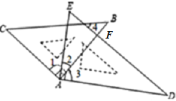
由题意可知∠CAB=∠EAD=90°，∠B=∠C=45°，∠D=30°，∠E=60°，
∵∠1+∠2=∠2+∠3=90°，
∴∠1=∠3，故①正确；
若BC∥AD，
∠3与∠4既不是同位角，也不是内错角，无法证明∠4=∠3，故②错误；
若∠2=15°，
∴∠EFB=∠2+∠E=15°+60°=75°，
∴∠4=180°﹣∠EFB﹣∠B=180°﹣75°﹣45°=60°，
∵∠D=30°，
∴∠4=2∠D，故③正确；
若∠2=30°，则∠1=∠3=90°﹣30°=60°，
∴∠CAD=∠1+∠2+∠3=150°，
∵∠CAD+∠D=150°+30°=180°，
∴AC∥DE（同旁内角互补，两直线平行）.故④正确.
故答案为：①③④.
练习册系列答案
相关题目
【题目】有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克） |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐重______千克；
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价
元，则出售这20筐白菜可卖多少元？
