��Ŀ����
����Ŀ�����壺��һ���ڱ���ȣ��������ǵļн���ֱ�ǵ��ı��ν�������ֱ���ı���.
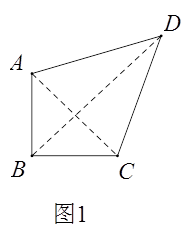
��1����ͼ1������ֱ���ı���ABCD��AB=BC����ABC=90�㣬
����AB=CD=1��AB//CD����Խ���BD�ij�.
����AC��BD����֤��AD=CD.
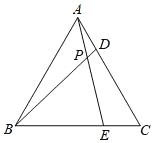
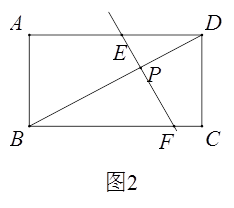
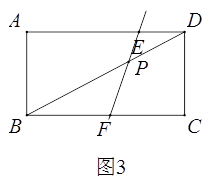
��2����ͼ2���ھ���ABCD�У�AB=5��BC=9����P�ǶԽ���BD��һ�㣬��BP=2PD������P��ֱ�߷ֱ�AD��BC�ڵ�E��F��ʹ�ı���ABFE�ǵ���ֱ���ı���.��AE�ij�.
���𰸡�
��1��
�⣺����ΪAB=CD=1��AB//CD,
�����ı���ABCD��ƽ���ı���.
����ΪAB=BC��
������ABCD������.
����Ϊ��ABC=90�ȣ�
��������ABCD��������.
����BD= ![]() .
.
����ͼ1������AC��BD��
��ΪAB=BC��AC��BD��
���ԡ�ABD=��CBD,
����ΪBD=BD��
���ԡ�ABD��CBD��
����AD=CD.
��2��
�⣺��EF��BC��ֱ����AE��EF��BF��EF��
�����ı���ABFE���ǵ���ֱ���ı��Σ�������������
��EF��BC����ֱ��
�ٵ�AE=ABʱ����ͼ2��
��ʱ�ı���ABFE�ǵ���ֱ���ı���.
����AE=AB=5.
�ڵ�BF=ABʱ����ͼ3��
��ʱ�ı���ABFE�ǵ���ֱ���ı���.
����BF=AB=5��
��ΪDE//BF��
���ԡ�PED~��PFB��
����DE��BF=PD��PB=1:2,
����AE=9-2.5=6.5.
����������AE�ij�Ϊ5��6.5.
����������1������AB=CD=1��AB//CD,���ݡ���һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Ρ��ɵ��ı���ABCD��ƽ���ı���.���ڱ����AB=BC����һֱ�ǡ�ABC=90�ȣ���������ABCD��������.��BD= ![]() ��������AC��BD����AB=BC��AC��BD����֪�ı���ABCD��һ�����Σ���ֻҪ֤����ABD��CBD�����ɵõ�AD=CD.��2���������ۣ���EF��BC��ֱ����ʾ��AE��EF��BF��EF����EF�������ڱ߲���ȣ��ɡ�A=��ABC=90�㣬�ɷ�������AB=AEʱ��AB=BFʱȥ���.
��������AC��BD����AB=BC��AC��BD����֪�ı���ABCD��һ�����Σ���ֻҪ֤����ABD��CBD�����ɵõ�AD=CD.��2���������ۣ���EF��BC��ֱ����ʾ��AE��EF��BF��EF����EF�������ڱ߲���ȣ��ɡ�A=��ABC=90�㣬�ɷ�������AB=AEʱ��AB=BFʱȥ���.
�����㾫����������Ĺؼ���������ƽ���ı��ε��ж������֪ʶ����������Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı��Σ�