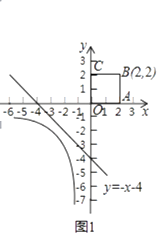��Ŀ����
����Ŀ�������
���壺���ı��ε�ijЩ���������ӳ������������в����ӳ�����ֱ�ߵ�ͬһ�ԣ��������ı��ν������ı��Σ���ͼ1���ı���ABCDΪ���ı��Σ�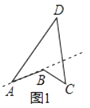
��1������̽��������ɰ��ı���һ�����ʵ�֤����
��֪����ͼ2���ı���ABCD�ǰ��ı��Σ�
��֤����BCD=��B+��A+��D��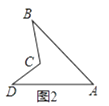
��2������Ӧ�ã�
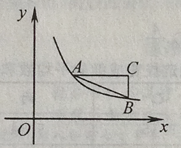
��ͼ3���ڰ��ı���ABCD�У���BAD�Ľ�ƽ�������BCD�Ľ�ƽ���߽��ڵ�E������ADC=140�㣬��AEC=102�㣬���B=�㣮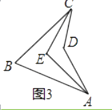
���𰸡�
��1��
�ӳ�BC��AD�ڵ�M
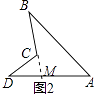
�ߡ�BCD�ǡ�CDM����ǣ�
���BCD=��CMD+��D��
ͬ����CD�ǡ�ABM����ǣ�
���CMD=��A+��B��
���BCD=��A+��B+��D��
��2��64
����������1���ӳ�BC��AD�ڵ�M�����������ε���ǵ����ʼ��ɽ�����⣮��2�����ã�1���н�����ͼ3�У����B=x����ECB=��ECD=������EAD=��EAB=�£��г������鼴�ɽ�����⣮
�����㾫����������Ĺؼ��������������ڽ�����ǵ����֪ʶ�����ն���ε��ڽǺͶ�����n���ε��ڽǺ͵��ڣ�n-2��180��.����ε���ǺͶ������������ε���Ǻ͵���360�㣮

����Ŀ��ijУ�ϳ�����30����Ա���±��Ǻϳ��ų�Ա������ֲ�ͳ�Ʊ���
���䣨��λ���꣩ | 13 | 14 | 15 | 16 |
Ƶ������λ������ | 5 | 15 | x | 10��x |
���ڲ�ͬ��x�����й��������ͳ�������ᷢ���ı���ǣ� ��
A.ƽ��������λ��
B.ƽ����������
C.���������
D.����������