题目内容
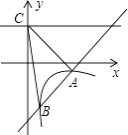
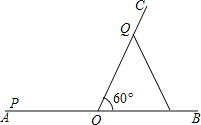
【题目】如图，∠BOC=60°，点A是BO延长线上的一点，OA=10cm，动点P从点A出发沿AB以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P，Q同时出发，用t（s）表示移动的时间，当t=________s时，△POQ是等腰三角形；当t=_______s时，△POQ是直角三角形．
【答案】
或10 
【解析】
根据△POQ是等腰三角形，分两种情况进行讨论：点P在AO上，或点P在BO上；根据△POQ是直角三角形，分两种情况进行讨论：PQ⊥AB，或PQ⊥OC，据此进行计算即可．
如图，当PO=QO时，△POQ是等腰三角形
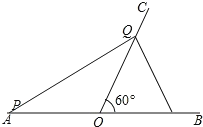
∵PO=AOAP=102t，OQ=1t
∴当PO=QO时，102t=t
解得t=；
如图，当PO=QO时，△POQ是等腰三角形
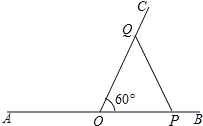
∵PO=APAO=2t10，OQ=1t
∴当PO=QO时，2t10=t
解得t=10；
如图，当PQ⊥AB时，△POQ是直角三角形，且QO=2OP
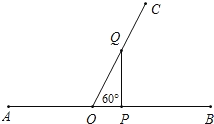
∵PO=APAO=2t10，OQ=1t，
∴当QO=2OP时,t=2×(2t10)
解得t=；
如图，当PQ⊥OC时，△POQ是直角三角形，且2QO=OP
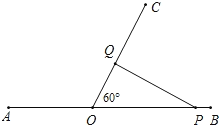
∵PO=APAO=2t10，OQ=1t，
∴当2QO=OP时，2t=2t10
方程无解.
故答案为：(1). 或10 (2).
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
【题目】有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克） |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐重______千克；
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价
元，则出售这20筐白菜可卖多少元？
【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y+2）（y+6）+4 （第一步）
=y2+8y+16 （第二步）
=（y+4）2（第三步）
=（x2－4x+4）2（第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式 |
B．平方差公式 |
C．两数和的完全平方公式 |
D．两数差的完全平方公式 |
（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．
（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．
