题目内容
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、点
、点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;直线
;直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是第一象限内抛物线上一动点.
是第一象限内抛物线上一动点.
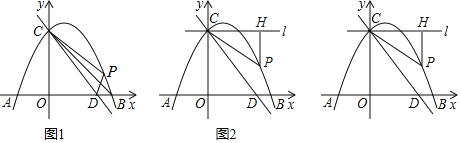
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)如图2,过点![]() 作直线
作直线![]() 轴,过点
轴,过点![]() 作
作![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 的对应点
的对应点![]() 恰好落在直线
恰好落在直线![]() 上,同时使点
上,同时使点![]() 的对应点
的对应点![]() 恰好落在坐标轴上,请直接写出此时点
恰好落在坐标轴上,请直接写出此时点![]() 的坐标.
的坐标.
【答案】(1) y=-![]() x2+x+4 (2)
x2+x+4 (2) ![]() (3) 点P坐标为(
(3) 点P坐标为(![]() )或(
)或(![]() )
)
【解析】
(1)由于抛物线交y轴于点C,直线y=-![]() x+4也经过点C,令x=0代入直线即求得点C坐标.再用待定系数法即求出抛物线解析式.
x+4也经过点C,令x=0代入直线即求得点C坐标.再用待定系数法即求出抛物线解析式.
(2)由OB=OC可得∠OBC=45°,所以过点D作BC的垂线并交直线CP于点F,可证得∠OBF=45°,即得到点F横坐标与B相等,纵坐标=BF=BD,由直线CD解析式求得点D即求出BD的长,进而得点F坐标,可求直线CP解析式.把直线CP解析式与抛物线解析式联立方程组即求得点P坐标.求直线CP与x轴交点G,可得△PCD面积等于△CDG面积减去△PDG面积,代入计算即求得△PCD面积.
(3)由于点P'落在坐标轴上,故有两种情况需分类讨论.①当点P'在y轴上时,由∠PCH=∠P'CH'与∠OCB=∠BCH=45°可得∠DCB=∠PCB,由第(2)可知此时P(![]() ,
,![]() ).②当点P'在x轴上时,设点P横坐标为p,则能用p表示P'H'、CH'.过点H'作x轴的垂线MN,证得∠H'P'M=∠CH'N=∠OCD,则由∠OCD的三角函数值可求得用p表示的MH'即列方程,进而求得p的值.
).②当点P'在x轴上时,设点P横坐标为p,则能用p表示P'H'、CH'.过点H'作x轴的垂线MN,证得∠H'P'M=∠CH'N=∠OCD,则由∠OCD的三角函数值可求得用p表示的MH'即列方程,进而求得p的值.
(1)∵当x=0时,y=-![]() x+4=4
x+4=4
∴C(0,4)
∵抛物线y=-![]() x2+bx+c过点B(4,0)、C(0,4)
x2+bx+c过点B(4,0)、C(0,4)
∴![]() 解得:
解得:![]()
∴抛物线解析式为y=-![]() x2+x+4
x2+x+4
(2)如图1,直线CP与x轴交于点G,过点D作DE⊥CB于点E,交直线CP于点F,连接BF.
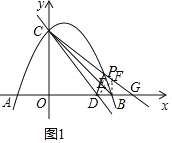
∴∠CED=∠CEF=90°
在△CDE与△CFE中
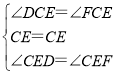
∴△CDE≌△CFE(ASA)
∴DE=FE,即BC垂直平分DF
∴BD=BF
∵B(4,0),C(0,4)
∴∠OBC=45°
∴∠CBF=∠OBC=45°
∴∠DBF=90°
∵当y=-![]() x+4=0时,解得:x=3
x+4=0时,解得:x=3
∴D(3,0)
∴BF=BD=4-3=1
∴F(4,1)
设直线CF解析式为y=kx+4
∴4k+4=1 解得:k=-![]()
∴直线CP:y=-![]() x+4
x+4
当y=0时,-![]() x+4=0,解得:x=
x+4=0,解得:x=![]()
∴G(![]() ,0),DG=
,0),DG=![]() -3=
-3=![]()
∵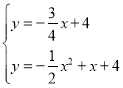
解得: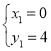 (即点C),
(即点C),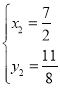
∴P(![]() )
)
∴S△PCD=S△CDG-S△PDG=![]() DGOC-
DGOC-![]() DGyP=
DGyP=![]() DG(OC-yP)=
DG(OC-yP)=![]() ×
×![]() ×(4-
×(4-![]() )=
)=![]()
∴△PCD的面积为![]()
(3)①若点P'落在y轴上,如图2,
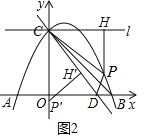
∵△CPH绕点C旋转得△CP'H',H'在直线CD上
∴∠PCH=∠PCH'
∵∠OCB=∠BCH=45°
∴∠OCB-∠OCH'=∠BCH-∠PCH
即∠DCB=∠PCB
由(2)可得此时点P(![]() )
)
②若点P'落在x轴上,如图3,过点H'作MN⊥x轴于点M,交直线l于点N
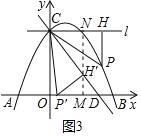
∴四边形OCNM是矩形
∴MN=OC=4,
∵OD=3,∠COD=90°
∴CD=![]()
∴sin∠OCD=![]() ,cos∠OCD=
,cos∠OCD=![]() ,
,
设点P坐标(p,-![]() p2+p+4)(0<p<4)
p2+p+4)(0<p<4)
∴CH'=CH=p,P'H'=PH=4-(-![]() p2+p+4)=
p2+p+4)=![]() p2-p
p2-p
∵MN∥y轴
∴∠CH'N=∠OCD
∴Rt△CNH'中,cos∠CH'N= ![]()
∴NH'=![]() CH'=
CH'=![]() p
p
∴MH'=MN-NH'=4-![]() p
p
∵∠P'MH'=∠P'H'C=90°
∴∠P'H'M+∠CH'N=∠P'H'M+∠H'P'M=90°
∴∠H'P'M=∠CH'N
∴Rt△H'P'M中,sin∠H'P'M=![]()
∴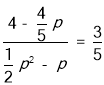
解得:p1=-4(舍去),p2=![]()
∴-![]() p2+p+4=-
p2+p+4=-![]()
∴P(![]() )
)
综上所述,点P坐标为(![]() )或(
)或(![]() )
)

 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案