题目内容
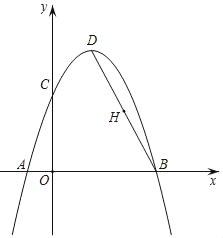
【题目】已知:二次函数y=﹣2x2+4x+m+1,与x轴的公共点为A,B.
(1)如果A与B重合,求m的值;
(2)横、纵坐标都是整数的点叫做整点:
①当m=﹣1时,求线段AB上整点的个数;
②若设抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n,当1<n≤8时,结合函数的图象,求m的取值范围.
【答案】(1)-3(2)①当m=﹣1时,线段AB上整点的个数有3个②﹣3<m≤0
【解析】
(1)当A、B重合时,抛物线与x轴只有一个交点,此时△=0,从可求出m的值.
(2)①m=﹣1代入抛物线解析式,然后求出该抛物线与x轴的两个交点的坐标,从而可求出线段AB上的整点个数.
②由图象可得![]() ,即可求出m的取值范围.
,即可求出m的取值范围.
(1)∵A与B重合,
∴二次函数y=﹣2x2+4x+m+1的图象与x轴只有一个公共点,
∴方程﹣2x2+4x+m+1=0有两个相等的实数根,
∴△=42+4×2(m+1)=24+8m=0,
解得:m=﹣3.
∴如果A与B重合,m的值为-3.
(2)①当m=﹣1时,原二次函数为y=﹣2x2+4x+m+1=﹣2x2+4x,
令y=﹣2x2+4x=0,则x1=0,x2=2,
∴线段AB上的整点有(2,0)、(1,0)和(0,0).
故当m=﹣1时,线段AB上整点的个数有3个.
②二次函数![]() ,
,
当![]() 时,
时,![]()
由点A,B之间的部分与线段AB所围成的区域内(包括边界)如图:
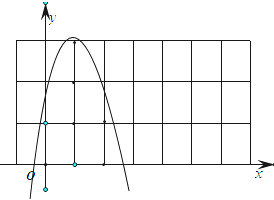
当![]() 时,
时,
∴![]()
∴![]() .
.

【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
10 | 10 | 500 |
15 | 20 | 900 |
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?