题目内容
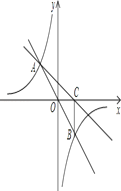
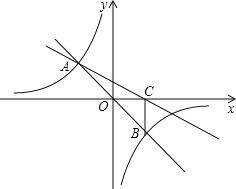
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式.
(3)点P在双曲线上,且△POC的面积等于△ABC面积的![]() ,求点P的坐标。
,求点P的坐标。
【答案】(1)m=-2,n=-2(2)y=-x+1(3)(2,-1)或(-2,1)
【解析】
(1)由题意,根据对称性得到B的横坐标为1,确定出C的坐标,根据三角形AOC的面积求出A的纵坐标,确定出A坐标,将A坐标代入一次函数与反比例函数解析式,即可求出m与n的值;
(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出直线AC的解析式.
(3)根据双曲线的对称性求得B(1,-2),求出三角形ABC的面积,设点P(a,![]() ),再根据S△POC=
),再根据S△POC=![]() S△ABC,列出关于a的方程即可。
S△ABC,列出关于a的方程即可。
(1)∵直线y=mx与双曲线y=![]() 相交于A(-1,a)、B两点,
相交于A(-1,a)、B两点,
∴B点横坐标为1,∵BC⊥x轴,则C(1,0),
∵△AOC的面积为1,
∴A(-1,2),
将A(-1,2)代入y=mx,y=![]() 可得m=-2,n=-2;
可得m=-2,n=-2;
(2)设直线AC的解析式为y=kx+b,
∵y=kx+b经过点A(-1,2)、C(1,0)
∴![]() ,
,
解得k=-1,b=1,
∴直线AC的解析式为y=-x+1;
(3)由对称性可得B(1,-2),
∴S△ABC=![]() =2,
=2,
设点P(a,![]() ),
),
∵S△POC=![]() S△ABC,
S△ABC,
∴S△POC=![]() ,
,
解得a=2或-2,
∴点P的坐标为(2,-1)或(-2,1).

【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.