题目内容
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲,乙,丙三名校排球队员每人10次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.

(1)若运动员丙测试成绩的平均数和众数都是7,则成绩统计表中a= ,b= ;
(2)若在三名队员中选择一位垫球成绩优秀且较为稳定的同学作为排球比赛的自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() ,
,![]() ,
,![]() )
)
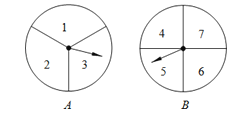
(3)训练期间甲、乙、丙三人之间进行随机传球游戏,先由甲传出球,经过三次传球,球回到甲手中的概率是多少?
【答案】(1)7;7 (2)见解析 (3)![]()
【解析】
(1)先根据众数的概念确定b的值,再利用平均数的概念列出求出a的值;
(2)计算出三人成绩的平均数,众数,结合方差的意义判断即可;
(3)画出树状图,然后根据概率公式列式进行计算即可得解.
(1)∵众数为7,
∴![]() ,
,
又平均数为7,
∴![]() ,
,
解得![]() ,
,
故答案为:7,7;
(2)甲的平均数为:![]() (分),众数是6(分);
(分),众数是6(分);
乙的平均数为:![]() (分),众数是7(分);
(分),众数是7(分);
丙的平均数为:![]() (分)众数是7(分);
(分)众数是7(分);
从平均数上看,乙和丙较高,从众数上看也是乙和丙较高;但是![]() <
<![]() ,
,
因此,综合考虑选乙更合适;
(3)画树状图如下:
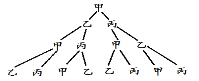
一共有8种可能,最后球传回到甲手中的情况有2种可能,
∴经过三次传球,球回到甲手中的概率是![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8