ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+2ЃЈaЁй0ЃЉгыxжсНЛгкAЃЈ4ЃЌ0ЃЉЁЂBЃЈЉ1ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНКЭЖЅЕузјБъЃЛ
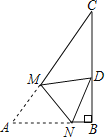
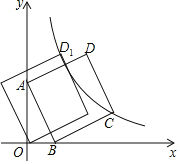
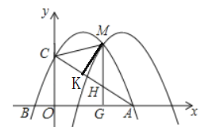
ЃЈ2ЃЉАбЃЈ1ЃЉжаЫљЧѓГіЕФХзЮяЯпМЧЮЊC1ЃЌНЋC1ЯђгвЦНвЦmИіЕЅЮЛЕУЕНХзЮяЯпC2ЃЌC1гыC2ЕФдкЕквЛЯѓЯоНЛЕуЮЊMЃЌЙ§ЕуMзїMK![]() гкKЃЌMGЁЭxжсгкЕуGЃЌНЛЯпЖЮACгкЕуHЃЌСЌНгCMЃЎ
гкKЃЌMGЁЭxжсгкЕуGЃЌНЛЯпЖЮACгкЕуHЃЌСЌНгCMЃЎ
ЂйЧѓЯпЖЮMKГЄЖШЕФзюДѓжЕЃЛ
ЂкЕБЁїCMHЮЊЕШбќШ§НЧаЮЪБЃЌЧѓХзЮяЯпЯђгвЦНвЦЕФОрРыmКЭДЫЪБЕуMЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ(
ЃЛ(![]() ЃЈ2ЃЉЂй
ЃЈ2ЃЉЂй![]() ЂкЕБmЃН1ЪБЃЌMЃЈ2ЃЌ3ЃЉЃЛЕБmЃН5Љ2
ЂкЕБmЃН1ЪБЃЌMЃЈ2ЃЌ3ЃЉЃЛЕБmЃН5Љ2![]() ЪБЃЌM
ЪБЃЌM![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
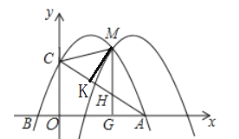
ЃЈ1ЃЉРћгУЕуAЃЌBЕФзјБъЕУЕНХзЮяЯпЕФНтЮіЪНЃЌВЂНЋЦфећРэГЩЖЅЕуЪНЃЌМДПЩЕУЖЅЕузјБъЃЛ
ЃЈ2ЃЉЂйЙиМќЪЧжЄУї![]() Ёз
Ёз![]() ЕУЕНMK=
ЕУЕНMK=![]() ЃЌЛЏаБЮЊжБЃЌжЛашMHГЄЖШзюДѓЪБЃЌMKГЄЖШзюДѓЃЌЩшM(xЃЌЉ
ЃЌЛЏаБЮЊжБЃЌжЛашMHГЄЖШзюДѓЪБЃЌMKГЄЖШзюДѓЃЌЩшM(xЃЌЉ![]() x2+
x2+![]() +2ЃЉ,H(xЃЌЉ
+2ЃЉ,H(xЃЌЉ![]() x+2ЃЉЃЌMHГЄЖШЕФзюДѓжЕзЊЛЏЮЊЖўДЮКЏЪ§ЕФзюжЕЮЪЬтМДПЩЧѓНтЃЛ
x+2ЃЉЃЌMHГЄЖШЕФзюДѓжЕзЊЛЏЮЊЖўДЮКЏЪ§ЕФзюжЕЮЪЬтМДПЩЧѓНтЃЛ
ЂкЁїCMHЮЊЕШбќШ§НЧаЮЃЌЗжШ§жжЧщПіЃКЃЈЂЁЃЉЕБCMЃНCHЪБЃЌЃЈiiЃЉЕБHCЃНHMЪБ,ЃЈiiiЃЉЕБCMЃНHMЪБЃЌЗжБ№РћгУЦфЯргІЕФМИКЮЬиеїНЈСЂЗНГЬЧѓНтЕУЕНЕуMЕФзјБъЃЌДњШыЦНвЦКѓЕФНтЮіЪНжаЧѓЕУmЕФжЕЃЎ
НтЃКЃЈ1ЃЉЕБxЃН0ЪБЃЌyЃНax2+bx+2ЃН2ЃЌ
ЁрХзЮяЯпОЙ§ЃЈ0ЃЌ2ЃЉЃЌ
ЁпХзЮяЯпyЃНax2+bx+2ЃЈaЁй0ЃЉгыxжсНЛгкAЃЈ4ЃЌ0ЃЉЁЂBЃЈЉ1ЃЌ0ЃЉСНЕуЃЌ
ЩшХзЮяЯпЕФБэДяЪНЮЊЃКyЃНaЃЈxЉ4ЃЉЃЈx+1ЃЉЃЌ
АбЃЈ0ЃЌ2ЃЉДњШыЕУЃК2ЃНaЃЈ0Љ4ЃЉЃЈ0+1ЃЉЃЌ
aЃНЉ![]() ЃЌ
ЃЌ
ЁрyЃНЉ![]() ЃЈxЉ4ЃЉЃЈx+1ЃЉЃНЉ
ЃЈxЉ4ЃЉЃЈx+1ЃЉЃНЉ![]() x2+
x2+![]() +2ЃНЉ
+2ЃНЉ![]() ЃЈxЉ
ЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФБэДяЪНЮЊЃК![]() ЃЌЖЅЕузјБъЪЧ(
ЃЌЖЅЕузјБъЪЧ(![]()
(2)ЂйЩшжБЯпACЕФБэДяЪНЮЊЃКyЃНkx+bЃЌ
АбAЃЈ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ2ЃЉДњШыЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК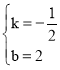 ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊЃКyЃНЉ![]() x+2ЃЌ
x+2ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]()
![]() Ёз
Ёз![]() ЃЌ
ЃЌ
![]()
![]()
![]() ЃЌ
ЃЌ
ЩшM(xЃЌЉ![]() x2+
x2+![]() +2ЃЉ,H(xЃЌЉ
+2ЃЉ,H(xЃЌЉ![]() x+2ЃЉгЩЬтжЊ
x+2ЃЉгЩЬтжЊ![]()
![]() MK=
MK=![]() =
=![]() [Љ
[Љ![]() x2+
x2+![]() +2-(Љ
+2-(Љ![]() x+2)]=
x+2)]=![]() [-
[-![]() ]
]
ЕБx=2ЪБЃЌMKзюДѓЕШгк![]()
ЂкЁпЁїCMHЮЊЕШбќШ§НЧаЮЃЌЗжШ§жжЧщПіЃК
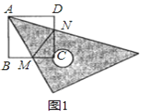
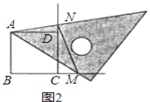
ЃЈЂЁЃЉЕБCMЃНCHЪБЃЌCЪЧMHДЙжБЦНЗжЯпЩЯЕФЕуЃЌЙ§ЕуCзїCPЁЭMHЃЌдђMP=PHЃЌ
ЧвгЩЭМПЩжЊOC=PG=2
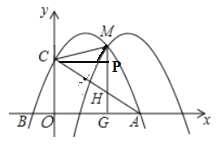
ЁрGH+GM=PG-PH+PG+MP=2PG=2OC
ЁрGH+GMЃН4ЃЌ
дђЉ![]() x2+
x2+![]() +2+ЃЈЉ
+2+ЃЈЉ![]() x+2ЃЉЃН4ЃЌНтЕУЃКx1ЃН0ЃЈЩсЃЉЃЌx2ЃН2ЃЌ
x+2ЃЉЃН4ЃЌНтЕУЃКx1ЃН0ЃЈЩсЃЉЃЌx2ЃН2ЃЌ
ЁрMЃЈ2ЃЌ3ЃЉЃЌ
ЩшЦНвЦКѓЕФХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЉ![]() ЃЈxЉ
ЃЈxЉ![]() ЉmЃЉ2+
ЉmЃЉ2+![]() ЃЌ
ЃЌ
АбMЃЈ2ЃЌ3ЃЉДњШыЕУЃКmЃН1ЃЎ
ЃЈЂЂЃЉЕБHCЃНHMЪБЃЌHMЃНЉ![]() x2+
x2+![]() x+2ЉЃЈЉ
x+2ЉЃЈЉ![]() x+2ЃЉЃНЉ
x+2ЃЉЃНЉ![]() x2+2xЃЌ
x2+2xЃЌ
CH2ЃН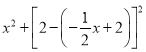 ЃЌCHЃН
ЃЌCHЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃНЉ
ЃНЉ![]() x2+2xЃЌНтЕУx1ЃН0ЃЈЩсЃЉЃЌx2ЃН4Љ
x2+2xЃЌНтЕУx1ЃН0ЃЈЩсЃЉЃЌx2ЃН4Љ![]() ЃЌ
ЃЌ
ЁрMЃЈ4Љ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшЦНвЦКѓЕФХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЉ![]() ЃЈxЉ
ЃЈxЉ![]() ЉmЃЉ2+
ЉmЃЉ2+![]() ЃЌ
ЃЌ
АбMЃЈ4Љ![]() ЃЌЉ
ЃЌЉ![]() ЃЉДњШыЕУЃКm1ЃН0ЃЈЩсЃЉЃЌm2ЃН5Љ2
ЃЉДњШыЕУЃКm1ЃН0ЃЈЩсЃЉЃЌm2ЃН5Љ2![]() ЃЛ
ЃЛ
ЃЈЂЃЃЉЕБCMЃНHMЪБЃЌHMЃНЉ![]() x2+2xЃЌCM2ЃН
x2+2xЃЌCM2ЃН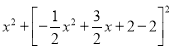 ЃЌ
ЃЌ
дђ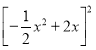 ЃН
ЃН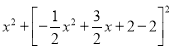 ЃЌ НтЕУxЃН
ЃЌ НтЕУxЃН![]() ЃЌ
ЃЌ
ЁрMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшЦНвЦКѓЕФХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЉ![]() ЃЈxЉ
ЃЈxЉ![]() ЉmЃЉ2+
ЉmЃЉ2+![]() ЃЌ
ЃЌ
АбMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉДњШыЕУЃКmЃН0ЃЈЩсЃЉЃЛ
ЃЉДњШыЕУЃКmЃН0ЃЈЩсЃЉЃЛ
злЩЯЫљЪіЃЌЕБmЃН1ЪБЃЌMЃЈ2ЃЌ3ЃЉЃЛЕБmЃН5Љ2![]() ЪБЃЌMЃЈ4Љ
ЪБЃЌMЃЈ4Љ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ

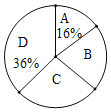
ЁОЬтФПЁП2020Фъ4дТЪЧЮвЙњЕк32ИіАЎЙњЮРЩњдТЃЎФГаЃОХФъМЖЭЈЙ§ЭјПЮОйааСЫжїЬтЮЊЁАЗРвпгаЮвЃЌАЎЮРЭЌааЁБЕФжЊЪЖОКШќЛюЖЏЃЎЮЊСЫНтШЋФъМЖ500УћбЇЩњДЫДЮОКШќГЩМЈЃЈАйЗжжЦЃЉЕФЧщПіЃЌЫцЛњГщШЁСЫВПЗжВЮШќбЇЩњЕФГЩМЈЃЌећРэВЂЛцжЦГіШчЯТВЛЭъећЕФЭГМЦБэЃЈБэ1ЃЉКЭЭГМЦЭМЃЈШчЭМЃЉЃЎЧыИљОнЭМБэаХЯЂНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщвЛЙВЫцЛњГщШЁСЫ____ИіВЮШќбЇЩњЕФГЩМЈЃЛ
ЃЈ2ЃЉБэ1жаaЃН__ЃЛ
ЃЈ3ЃЉЫљГщШЁЕФВЮШќбЇЩњЕФГЩМЈЕФжаЮЛЪ§ТфдкЕФЁАзщБ№ЁБЪЧ__ЃЛ
ЃЈ4ЃЉЭГМЦЭМжаBзщЫљеМЕФАйЗжБШЪЧ_______ЃЛ
ЃЈ5ЃЉЧыФуЙРМЦЃЌИУаЃОХФъМЖОКШќГЩМЈДяЕН80ЗжвдЩЯЃЈКЌ80ЗжЃЉЕФбЇЩњШЫЪ§ЃЎ
Бэ1 жЊЪЖОКШќГЩМЈЗжзщЭГМЦБэ
зщБ№ | ЗжЪ§/Зж | ЦЕЪ§ |
A | 60ЁмxЃМ70 | a |
B | 70ЁмxЃМ80 | 10 |
C | 80ЁмxЃМ90 | 14 |
D | 90ЁмxЃМ100 | 18 |