题目内容
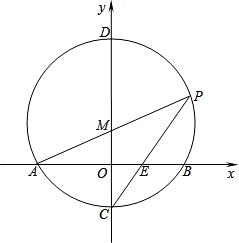
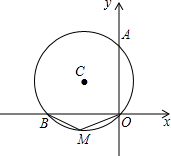
如图，在平面直角坐标系xOy中，△OCB的外接圆与y轴交于点A（0，
），∠OCB=60°，
∠COB=45°，求OC的长．
| 2 |
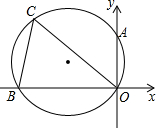
∠COB=45°，求OC的长．
连接AB
∵∠OCB=60°，
∴∠A=∠OCB=60°（1分）
∵A，(0，
)，∴OA=
在Rt△AOB中，tan∠BAO=
，
∴OB=
•tan60°=
×
=
（2分）
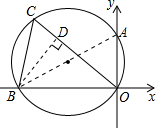
过点B作BD⊥OC于D，
∴∠CDB=∠BDO=90°
∵∠COB=45°，
∴∠DBO=∠COB=45°，∴OD=BD；（3分）
在Rt△DOB中，由勾股定理得OD=BD=
（4分）
在Rt△BCD中，tanC=
，∠C=60°，
∴CD=
=
=1（5分）
∴OC=OD+DC=
+1．（6分）
∵∠OCB=60°，
∴∠A=∠OCB=60°（1分）
∵A，(0，
| 2 |
| 2 |
在Rt△AOB中，tan∠BAO=
| BO |
| AO |
∴OB=
| 2 |
| 2 |
| 3 |
| 6 |
过点B作BD⊥OC于D，
∴∠CDB=∠BDO=90°
∵∠COB=45°，
∴∠DBO=∠COB=45°，∴OD=BD；（3分）
在Rt△DOB中，由勾股定理得OD=BD=
| 3 |
在Rt△BCD中，tanC=
| BD |
| CD |
∴CD=
| BD |
| tanC |
| ||
|
∴OC=OD+DC=
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
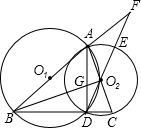⊙O1、⊙O2于B、C两点，延长DO2交⊙O2于E，交BA延长线于F，BO2交AD于G，连接AD．
