Question

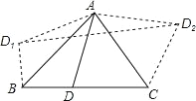
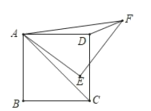
【题目】如图1，在Rt△ABC中，∠ABC＝90°，AB＝BC，将△ABC绕点A逆时针旋转，得到△ADE，旋转角为α（0°＜α＜90°），连接BD交CE于点F．

（1）如图2，当α＝45°时，求证：CF＝EF；

（2）在旋转过程中，①问（1）中的结论是否仍然成立？证明你的结论；②连接CD，当△CDF为等腰直角三角形时，求tan的值．

Answer 1

【答案】(1)见解析;(2) ① 成立,理由见解析;②

【解析】

(1)如图中，由∠EAC＝∠DAB，AE＝AC，AD＝AB，可得∠AEC＝∠ACE＝∠ADB＝∠ABD，继而可得FD＝FC，再根据∠EDC＝90°，继而可推导得出∠FED＝∠FDE，可得FE＝FD，即可求得EF＝FC；

(2)①如图1中，结论仍然成立．理由：连接AF，由旋转的性质可推导得出∠FCA＝∠ABF，从而可得A，B，C，F四点共圆，继而根据圆内接四边形的性质可求得∠AFC＝90°，有AF⊥EC，再根据AE＝AC，即可求得EF＝CF；

②分CF＝CD，∠FCD＝90°和DF＝DC，∠CDF＝90°两种情况分别进行讨论即可得.

(1)如图中，

∵∠EAC＝∠DAB，AE＝AC，AD＝AB，

∴∠AEC＝∠ACE＝∠ADB＝∠ABD，

∵∠ADB＝∠CDF，

∴∠FDC＝∠FCD，

∴FD＝FC，

∵∠EDC＝90°，

∴∠DEF+∠ECD＝90°，∠FDE+∠FDC＝90°，

∴∠FED＝∠FDE，

∴FE＝FD，

∴EF＝FC．

(2)①如图1中，结论仍然成立．

理由：连接AF．

∵AB=AD，AE=AC，

∴∠ABD=∠ADB，∠ACE=∠EAC，

又∵∠BAD=∠CAE，∠ABD+∠ADB+∠BAD=180°，∠ACE+∠EAC+∠CAE=180°，

∴∠FCA＝∠ABF，

∴A，B，C，F四点共圆，

∴∠AFC+∠ABC＝180°，

∵∠ABC＝90°，

∴∠AFC＝90°，

∴AF⊥EC，

∵AE＝AC，

∴EF＝CF．

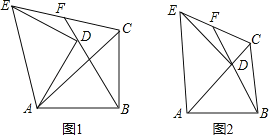
②如图3﹣1中，当CF＝CD，∠FCD＝90°时，连接AF，作CH⊥BF于H．设CF＝CD＝a．

则DE＝，DF＝a，

∵CF＝CD，CH⊥DF，

∴HF＝HD，

∴CH＝DF＝a，

∴BC＝DE＝a，

∴BH＝，

∵AE＝AC，EF＝CF，

∴AF平分∠EAC，

∵A，B，C，F四点共圆，

∴∠CAF＝∠CBH＝α，

∴tanα＝＝；

如图3﹣2中，当DF＝DC，∠CDF＝90°时，作DH⊥CF于H，连接AF．设CD＝DF＝m．

则CF＝EF＝a，DH＝CF＝m，

∴DE＝BC＝m，

∴BD＝＝2m，

∴tanα＝＝．