题目内容
根据下列表格中二次函数y＝ax2＋bx＋c的自变量
与函数值
的对应值,判断方程ax2＋b x＋c=0（a≠0）的一个解的范围是（ ）
| 6．17 | 6．18 | 6．19 | 6．20 |
| y＝ax2＋bx＋c | -0．03 | -0．01 |  |  |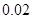
Ｃ．6．18＜x＜6．19 Ｄ．6．19＜x＜6．20
C．
解析试题分析:由表格中的数据看出﹣0.01和0.02更接近于0,故x应取对应的范围6．18＜x＜6．19．
故选C．
考点:抛物线与x轴的交点．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
二次函数
的顶点坐标是（ ）
| A．（1，-2） | B．（1，2） |
| C．（0，-2） | D．（0，2） |
把抛物线y=3x2沿y轴向上平移8个单位，所得抛物线的函数关系式为（ ）
| A．y=3x2+8 | B．y=3x2－8 | C．y=3(x+8) 2 | D．y=3(x－8) 2 |
如图是二次函数y=ax2+bx+c（a≠0）的图象，则下列说法中正确的是（）
| A．A＞0 | B．4a+b＞0 | C．c="0" | D．A+b+c＞0 |
在平面直角坐标系中，抛物线
的顶点是点P，对称轴与x轴相交于点Q，以点P为圆心，PQ长为半径画⊙P，那么下列判断正确的是（ ）
| A．x轴与⊙P相离； | B．x轴与⊙P相切； |
| C．y轴与⊙P与相切； | D．y轴与⊙P相交． |
如图，已知抛物线
与x轴分别交于O、A两点，它的对称轴为直线x=a，将抛物线
向上平移4个单位长度得到抛物线
，则图中两条抛物线、对称轴与y轴所围成的图形（图中阴影部分）的面积为
| A．4 | B．6 | C．8 | D．16 |
一小球被抛出后，距离地面的高度h（米）和飞行时间t（秒）满足下列函数关系式：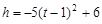
，则小球距离地面的最大高度是
| A．1米 | B．5米 | C．6米 | D．7米 |
和直线
.我们约定：当x任取一值时，x对应的函数值分别为y1、y2，若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2.下列判断：①当x＞2时，M=y2；②当x＜0时，x值越大，M值越大；③使得M大于4的x值不存在；④若M=2，则x=1.其中正确的有 （ ）
