题目内容
如图,已知抛物线 和直线
和直线 .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有 ( )
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
B.
解析试题分析:∵当y1=y2时,即 时,解得:x=0或x=2,
时,解得:x=0或x=2,
∴由函数图象可以得出当x>2时, y2>y1;当0<x<2时,y1>y2;当x<0时, y2>y1. ∴①错误.
∵当x<0时,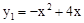 直线
直线 的值都随x的增大而增大,
的值都随x的增大而增大,
∴当x<0时,x值越大,M值越大. ∴②正确.
∵抛物线 的最大值为4,∴M大于4的x值不存在. ∴③正确.
的最大值为4,∴M大于4的x值不存在. ∴③正确.
∵当0<x<2时,y1>y2,∴当M=2时,2x=2,x=1;
∵当x>2时,y2>y1,∴当M=2时, ,解得
,解得 (舍去).
(舍去).
∴使得M=2的x值是1或 .∴④错误.
.∴④错误.
综上所述,正确的有②③2个.故选B.
考点:1.二次函数和一次函数的性质;2.曲线上点的坐标与方程的关系;3.数形结合和分类思想的应用.

练习册系列答案
相关题目
根据下列表格中二次函数y=ax2+bx+c的自变量 与函数值
与函数值 的对应值,判断方程ax2+b x+c=0(a≠0)的一个解
的对应值,判断方程ax2+b x+c=0(a≠0)的一个解 的范围是( )
的范围是( )
 | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 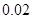 |  |
C.6.18<x<6.19 D.6.19<x<6.20
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列四个结论
①a、b同号
②当x=1和x=3时函数值相等
③4a+b=0
④当y= 时x的值只能取0
时x的值只能取0
其中正确的个数
| A.1个 | B.2个 | C.3个 | D.4个 |
将抛物线y=(x﹣1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
| A.y=(x﹣2)2 | B.y=(x﹣2)2+6 | C.y=x2+6 | D.y=x2 |
顶点为(-5,0)且平移后能与函数 的图象完全重合的抛物线是( )
的图象完全重合的抛物线是( )
A. | B. | C. | D. |
如图,抛物线 和直线
和直线 . 当y1>y2时,x的取值范围是( )
. 当y1>y2时,x的取值范围是( )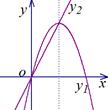
| A.0<x<2 | B.x<0或x>2 | C.x<0或x>4 | D.0<x<4 |
抛物线 与x轴的交点坐标是( )
与x轴的交点坐标是( )
| A.(1,0)(-3,0) | B.(-1,0)(3,0) |
| C.(1,0)(3,0) | D.(-1,0)(-3,0) |




 Rt
Rt (
( )的直角边与正方形
)的直角边与正方形 的边长均为2,且
的边长均为2,且 与
与 在同一直线上,开始时点
在同一直线上,开始时点 与点
与点 重合,让
重合,让 与点
与点 重合为止.设
重合为止.设 的长为
的长为 ,
, ,则
,则
