题目内容
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于E,以AE为直径作⊙O.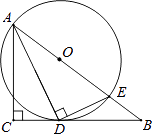
(1)求证:点D在⊙O上;
(2)求证:BC是⊙O的切线;
(3)若AC=6,BC=8,求△BDE的面积.
【答案】
(1)
证明:连接OD,
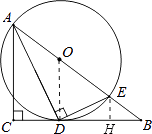
∵△ADE是直角三角形,OA=OE,
∴OD=OA=OE,
∴点D在⊙O上
(2)
证明:∵AD是∠BAC的角平分线,
∴∠CAD=∠DAB,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴AC∥OD,
∴∠C=∠ODB=90°,
∴BC是⊙O的切线
(3)
解:在Rt△ACB中,AC=6,BC=8,
∴根据勾股定理得:AB=10,
设OD=OA=OE=x,则OB=10﹣x,
∵AC∥OD,△ACB∽△ODB,
∴ ![]() ,∴
,∴ ![]() ,
,
解得:x= ![]() ,
,
∴OD= ![]() ,BE=10﹣2x=10﹣
,BE=10﹣2x=10﹣ ![]() =
= ![]() ,
,
∵ ![]() ,即
,即 ![]() ,
,
∴BD=5,
过E作EH⊥BD,
∵EH∥OD,
∴△BEH∽△BOD,
∴ ![]() ,
,
∴EH= ![]() ,
,
∴S△BDE= ![]() BDEH=
BDEH= ![]() .
.
【解析】(1)连接OD,由DO为直角三角形斜边上的中线,得到OD=OA=OE,可得出点D在圆O上;(2)由AD为角平分线,得到一对角相等,再由OD=OA,利用等边对等角得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OD与AC平行,根据两直线平行同位角相等即可得到∠ODB为直角,即BC与OD垂直,即可确定出BC为圆O的切线;(3)过E作EH垂直于BC,由OD与AC平行,得到△ACB与△ODB相似,设OD=OA=OE=x,表示出OB,由相似得比例列出关于x的方程,求出方程的解得到x的值,确定出OD与BE的长,进而确定出BD的长,再由△BEH与△ODB相似,由相似得比例求出EH的长,△BED以BD为底,EH为高,求出面积即可.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线)的相关知识才是答题的关键.