题目内容
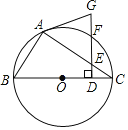
【题目】如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE=_____.
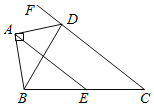
【答案】6
【解析】
取BD中点H,连AH、EH,根据角平分线和直角三角形斜边中线等于斜边一半,可得AH∥DF,又根据三角形中位线定理可得EH∥DC,可得A、H、E三点共线,进而可得AE的长.
解:如图,
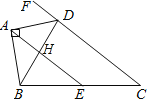
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=![]() BD=2.5,
BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=![]() CD=3.5,
CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
故答案为:6.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目