Question

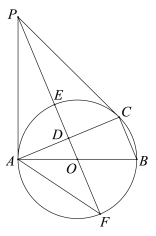
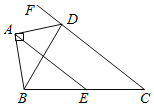
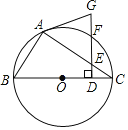
【题目】如图，△ABC为⊙O的内接三角形，BC为⊙O的直径，在线段OC上取点D（不与端点重合），作DG⊥BC，分别交AC、圆周于E、F，连接AG，已知AG＝EG．

（1）求证：AG为⊙O的切线；

（2）已知AG＝2，填空：

①当四边形ABOF是菱形时，∠AEG＝　 　°；

②若OC＝2DC，△AGE为等腰直角三角形，则AB＝　 　．

Answer 1

【答案】（1）证明见解析；（2）①60，②4．

【解析】

（1）连接OA，证明∠OAG=90°，即可证得AG为⊙O的切线；

（2）①连接OA，AF，OF，当四边形ABOF为菱形，则△AOB为等边三角形，从而求出∠ACB，∠DEC的度数，根据对顶角相等即可得到∠AEG的度数；

②若△AGE为等腰直角三角形，则可以得出△DEC, △ABC均为等腰三角形，通过证明四边形AODG是矩形，得到DC=AG，从而得到BC的长度，根据等腰直角三角形的性质，即可求出AB的长．

（1）证明：连接OA．

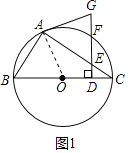
∵OA＝OC，

∴∠OAC＝∠OCA，

∵GA＝GE，

∴∠GAE＝∠GEA，

∵DG⊥BC，

∴∠EDC＝90°，

∴∠OCA+∠DEC＝90°，

∵∠CED＝∠GEA＝∠GAE，

∴∠OAC+∠GAE＝90°，

∴∠OAG＝90°，

∴OA⊥AG，

∴AG是⊙O的切线．

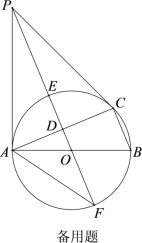
（2）①如图2中，连接OA，AF，OF．

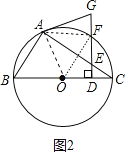
∵四边形ABOF是菱形，

∴AB＝BO＝OF＝AF＝OA，

∴△ABO是等边三角形，

∴∠B＝60°，

∵BC是直径，

∴∠BAC＝90°

∴∠ACB＝90°﹣60°＝30°，

∵ED⊥BC，

∴∠DEC＝90°﹣∠ACB＝60°，

∴∠AEG＝∠DEC＝60°．

故答案为60．

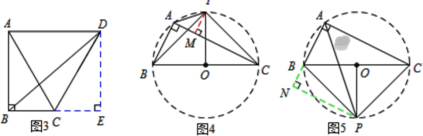
②如图3中，连接OA．

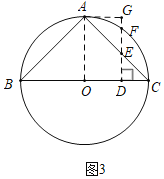
∵△AGE是等腰直角三角形，

∴∠AEG＝∠DEC＝∠DCE＝45°，

∴△EDC，△ABC都是等腰直角三角形，

∵OB＝OC，

∴AO⊥OC，

∴∠AOD＝∠ODG＝∠G＝90°，

∴四边形AODG是矩形，

∴AG＝OD＝2，

∴OC＝2OD＝4，

∴BC＝2OC＝8，

∴AB＝AC＝4，

故答案为4．