题目内容
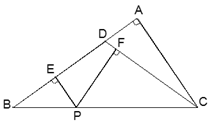
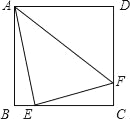
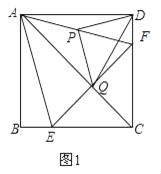
【题目】如图1,在正方形ABCD中,点E、F分别在边BC,CD上,且BE=DF,点P是AF的中点,点Q是直线AC与EF的交点,连接PQ,PD.
(1)求证:AC垂直平分EF;
(2)试判断△PDQ的形状,并加以证明;
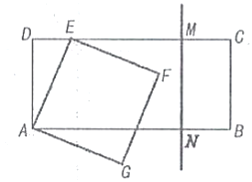
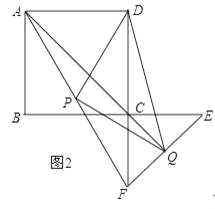
(3)如图2,若将△CEF绕着点C旋转180°,其余条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
【答案】(1)证明见解析;(2)△PDQ是等腰直角三角形;理由见解析(3)成立;理由见解析.
【解析】试题(1)由正方形的性质得出AB=BC=CD=AD,∠B=∠ADF=90°,∠BCA=∠DCA=45°,由BE=DF,得出CE=CF,△CEF是等腰直角三角形,即可得出结论;
(2)由直角三角形斜边上的中线的性质得出PD=![]() AF,PQ=
AF,PQ=![]() AF,得出PD=PQ,再证明∠DPQ=90°,即可得出结论;
AF,得出PD=PQ,再证明∠DPQ=90°,即可得出结论;
(3)由直角三角形斜边上的中线的性质得出PD=![]() AF,PQ=
AF,PQ=![]() AF,得出PD=PQ,再证明点A、F、Q、P四点共圆,由圆周角定理得出∠DPQ=2∠DAQ=90°,即可得出结论.
AF,得出PD=PQ,再证明点A、F、Q、P四点共圆,由圆周角定理得出∠DPQ=2∠DAQ=90°,即可得出结论.
试题解析:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠ADF=90°,∠BCA=∠DCA=45°,
∵BE=DF,
∴CE=CF,
∴AC垂直平分EF;
(2)解:△PDQ是等腰直角三角形;理由如下:
∵点P是AF的中点,∠ADF=90°,
∴PD=![]() AF=PA,
AF=PA,
∴∠DAP=∠ADP,
∵AC垂直平分EF,
∴∠AQF=90°,
∴PQ=![]() AF=PA,
AF=PA,
∴∠PAQ=∠AQP,PD=PQ,
∵∠DPF=∠PAD+∠ADP,∠QPF=∠PAQ+∠AQP,
∴∠DPQ=2∠PAD+2∠PAQ=2(∠PAD+∠PAQ)=2×45°=90°,
∴△PDQ是等腰直角三角形;
(3)成立;理由如下:
∵点P是AF的中点,∠ADF=90°,
∴PD=![]() AF=PA,
AF=PA,
∵BE=DF,BC=CD,∠FCQ=∠ACD=45°,∠ECQ=∠ACB=45°,
∴CE=CF,∠FCQ=∠ECQ,
∴CQ⊥EF,∠AQF=90°,
∴PQ=![]() AF=AP=PF,
AF=AP=PF,
∴PD=PQ=AP=PF,
∴点A、F、Q、P四点共圆,
∴∠DPQ=2∠DAQ=90°,
∴△PDQ是等腰直角三角形.