Question

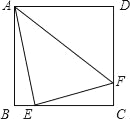
【题目】如图，在正方形ABCD中，点E，F分别在边BC，CD上，如果AE=4，EF=3，AF=5，那么正方形ABCD的面积等于_____．

Answer 1

【答案】

【解析】试题分析：根据△ABE∽△ECF，可将AB与BE之间的关系式表示出来，在Rt△ABE中，根据勾股定理AB2+BE2=AC2，可将正方形ABCD的边长AB求出，进而可将正方形ABCD的面积求出．

试题解析：设正方形的边长为x，BE的长为a

∵∠AEB+∠BAE=∠AEB+∠CEF=90°

∴∠BAE=∠CEF

∵∠B=∠C

∴△ABE∽△ECF

∴,即，

解得x=4a①

在Rt△ABE中，AB2+BE2=AE2

∴x2+a2=42②

将①代入②，可得：a=

∴正方形ABCD的面积为：x2=16a2=．