题目内容
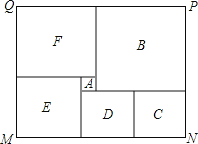
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,以
个单位的速度运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为![]() 秒,当
秒,当![]() ________.秒时,直线
________.秒时,直线![]() 和正方形
和正方形![]() 开始有公共点
开始有公共点
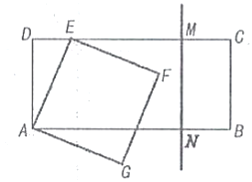
【答案】2
【解析】
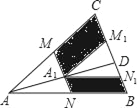
首先过点F作FQ⊥CD于点Q,证明△ADE≌△EQF,进而得出AD=EQ,得出当直线MN和正方形AEFG开始有公共点时:DQ+CM≥9,进而求解即可.
解:过点F作FQ⊥CD于点Q,则∠FQE=90,如图所示:
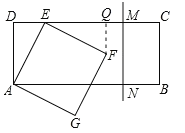
∵四边形ABCD为矩形,
∴∠D=90,
∴∠D=∠FQE,
∵在正方形AEFG中,∠AEF=90,AE=EF,
∴∠AED+∠QEF=90,
∵∠DAE+∠AED=90,
∴∠DAE=∠QEF,
在△ADE和△EQF中,
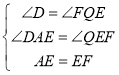
∴△ADE≌△EQF(AAS),
∴AD=EQ=3,
当直线MN和正方形AEFG开始有公共点时:DQ+CM9,
设当经过t秒时,直线MN和正方形AEFG开始有公共点,
则t+3+2t9,
解得:t2,
故答案为:2.

【题目】下列说法正确的有( )
①﹣a一定是负数;
②![]() 一定小于a;
一定小于a;
③互为相反数的两个数的绝对值相等;
④等式﹣a2=|﹣a2|一定成立;
⑤大于﹣3且小于2的所有整数的和是2.
A.0个B.1个C.2个D.3个
【题目】为了满足学生的物质需求,我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该红旗超市有几种进货方案?
(3)在(2)的条件下,该红旗超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?