题目内容
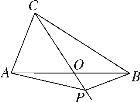
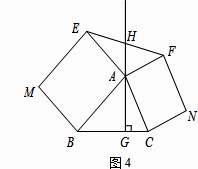
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
【答案】4![]()
【解析】结合已知AD:DB=1:4,BC=![]() ,应用勾股定理求出AC的长,连接PD,根据S△PBD+S△PCD=S△BCD,可得
,应用勾股定理求出AC的长,连接PD,根据S△PBD+S△PCD=S△BCD,可得![]() BDPE+
BDPE+![]() DCPF=
DCPF=![]() BDAC,继而得到PE+PF=AC即可得.
BDAC,继而得到PE+PF=AC即可得.
∵AD:DB=1:4,
∴设AD=n,BD=4n,
∴AB=5n,
∵DB=DC,∴DC=4n,
∵∠A=90°,∴AC2=DC2-AD2=15n2,AB2+AC2=BC2,
∵BC=4![]() ,
,
∴(5n)2+15n2=![]() ,
,
∴n2=![]() ,∴AC=
,∴AC=![]() =
=![]() ,
,
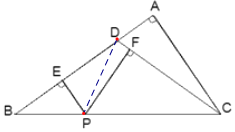
连接PD,PD把△BCD分成两个三角形△PBD,△PCD,
∵PE⊥AB ,PF⊥CD,AC⊥BD,
∴S△PBD=![]() BDPE,
BDPE,
S△PCD=![]() DCPF,
DCPF,
S△BCD=![]() BDAC,
BDAC,
∵S△PBD+S△PCD=S△BCD,
∴![]() BDPE+
BDPE+![]() DCPF=
DCPF=![]() BDAC,
BDAC,
∵DB=DC,
∴PE+PF=AC=![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目