题目内容
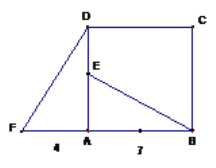
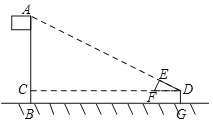
【题目】如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE=0.5m，EF=0.25m，目测点D到地面的距离DG=1.5m，到旗杆的水平距离DC=20m，则旗杆的高度为( )
A.
mB.
m
C.11.5mD.10m
【答案】C
【解析】
确定出△DEF和△DAC相似，根据相似三角形对应边成比例求出AC，再根据旗杆的高度=AC+BC计算即可得解．
解：∵∠FDE=∠ADC，
∠DEF=∠DCA=90°，
∴△DEF∽△DAC，
∴
，
即：
，
解得AC=10，
∵DF与地面保持平行，目测点D到地面的距离DG=1.5米，
∴BC=DG=1.5米，
∴旗杆的高度=AC+BC=10+1.5=11.5米．
故选：C．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
【题目】某课外学习小组根据学习函数的经验，对函数
的图象与性质进行了探究请补充完整以下探索过程：
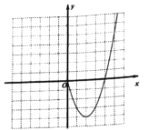
（1）列表：
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出
________，
________；
（2）根据上表中的数据，在平面直角坐标系内补全该函数的图象，并结合图象写出该函数的两条性质：
性质1______________________________________________________
性质2_______________________________________________________
（3）若方程
有四个不同的实数根，请根据函数图象，直接写出k的取值范围.
