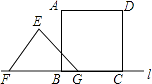Question

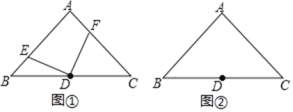
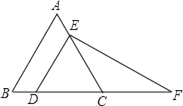
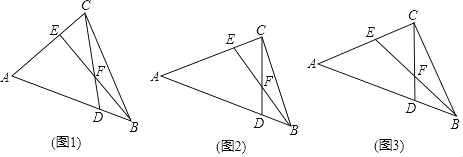
【题目】如图，在△ABC中，点D在边AB上，点E在边AC上，CE＝BD，连接CD，BE，BE与CD相交于点F．

（1）如图1，若△ACD为等边三角形，且CE＝DF，求∠CEF的度数；

（2）如图2，若AC＝AD，求证：EF＝FB；

（3）如图3，在（2）的条件下，若∠CFE＝45°，△BCD的面积为4，求线段CD的长．

Answer 1

【答案】（1）90°；（2）证明见解析；（3）4.

【解析】

（1）根据等边三角形的性质得到ADC=∠C=60°，根据三角形的外角的性质计算；

（2）作BG∥AC交CD的延长线于G，证明△CFE≌△GFB，根据全等三角形的性质证明；

（3）作EP⊥CD于P，BH⊥CD交CD的延长线于H，设EP=x，GH=a，根据全等三角形的性质得到BH=EP=x，根据三角形的面积公式计算．

（1）∵CE＝BD，CE＝DF，

∴BD＝DF，

∴∠DFB＝∠B，

∵△ACD为等边三角形，

∴∠ADC＝∠C＝60°，

∴∠DFB＝∠B＝30°，

∴∠CEF＝90°；

（2）证明：作BG∥AC交CD的延长线于G，

∴∠C＝∠G，

∵AC＝AD，

∴∠C＝∠ADC，

∴∠BDG＝∠G，

∴BD＝BG，

∵CE＝BD，

∴BD＝CE，

∵BG∥AC，

在△CFE和△GFB中，

，

∴△CFE≌△GFB，

∴EF＝FB；

（3）解：作EP⊥CD于P，BH⊥CD交CD的延长线于H，

设EP＝x，GH＝a，

∵∠CFE＝45°，

∴FP＝EP＝x，

∵△CFE≌△GFB，

∴BH＝EP＝x，

则FH＝BH＝x，

∵BD＝BG，BH⊥CD，

∴DH＝GH＝a，

∴CF＝FG＝x+a，DF＝x﹣a，

∴CD＝CF+DF＝2x，

由题意得，

×CD×BH＝4，即×2x×x＝4，

解得，x＝2，

则CD＝2x＝4．