题目内容
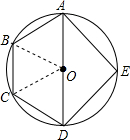
同圆的内接正三边形、正四边形、正六边形的边长之比为______.
设圆的半径为r,
如图①,∠AOB=
×360°=120°,
∵OA=OB,
∴∠OAB=30°,
过点O作OC⊥AB于点C,
则AB=2AC,
∵AC=OA•cos30°=
r,
∴AB=
r;
如图②,∠AOB=
×360°=90°,
∵OA=OB,
∴AB=
OA=
r;
如图③,∠AOB=
×360°=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴AB=OA=r;
∴同圆的内接正三边形、正四边形、正六边形的边长之比为:
:
:1.
故答案为:
:
:1.
如图①,∠AOB=
| 1 |
| 3 |
∵OA=OB,
∴∠OAB=30°,
过点O作OC⊥AB于点C,
则AB=2AC,
∵AC=OA•cos30°=
| ||
| 2 |
∴AB=
| 3 |
如图②,∠AOB=
| 1 |
| 4 |
∵OA=OB,
∴AB=
| 2 |
| 2 |
如图③,∠AOB=
| 1 |
| 6 |
∵OA=OB,
∴△OAB是等边三角形,
∴AB=OA=r;
∴同圆的内接正三边形、正四边形、正六边形的边长之比为:
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |


练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目