Question

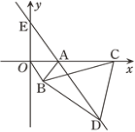
【题目】如图，直线y=kx+b与x轴，y轴分别交于A，B两点，且经过点(4，b+3).

(1)求k的值；

(2)若AB=OB+2,

①求b的值；

②点M为x轴上一动点，点N为坐标平面内另一点.若以A，B，M，N为顶点的四边形是菱形，请直接写出所有符合条件的点N的坐标.

Answer 1

【答案】(1)k=；(2)①b=3；②N(5,3)或(-5,3)或(0，-3)或(，3).

【解析】

（1）把点(4，b+3)的坐标代入直线解析式即可解答.

(2)根据x轴、y轴上点的坐标特征，用含b的式子表示点A、B的坐标，从而表示出OA、OB的长，根据勾股定理得出AB，代入AB=OB+2,得到关于b的方程，求解即可.

（3）根据菱形的性质：四边相等，对角线互相垂直平分、对边平行即可解答.

(1)由题知4k+b=b+3，∴4k=3，∴k=；

(2)①由(1)知AB:y=x+b，当x=0时，y=b，∴B(0，b).当y=x+b=0时，解得x=，∴A(，0)，∴OA=，OB=b，∴AB==，

∵AB=OB+2,∴=b+2，解得b=3.

②N(5,3)或(-5,3)或(0，-3)或(-，3).