题目内容
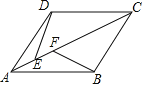
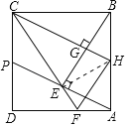
【题目】如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF.下列结论正确的是( )

A. CE=![]() B. EF=
B. EF=![]() C. cos∠CEP=
C. cos∠CEP=![]() D. HF2=EFCF
D. HF2=EFCF
【答案】D
【解析】
首先证明AH=HB,推出BG=EG,推出CB=CE,再证明△CBH≌△CEH,Rt△HFE≌Rt△HFA,利用全等三角形的性质即可一一判断.
连接![]() .
.
![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
∴CD=AB=BC=AD=2,CD∥AB,
∵BE⊥AP,CG⊥BE,
∴CH∥PA,
∴四边形![]() 是平行四边形,
是平行四边形,
∴CP = AH,
∵CP=PD=1,
∴AH=PC=1,
∴AH=BH,
在Rt△ABE中,∵AH=HB,
∴EH=HB,∵HC⊥BE,
∴BG=EG,
∴CB=CE=2,故选项A错误,
∵CH=CH,CB=CE,HB=HE,
∴△CBH≌△CEH,
∴∠CBH=∠CEH=90°,
∵HF=HF,HE=HA,
∴Rt△HFE≌Rt△HFA,
∴AF=EF,设EF=AF=x,
在Rt△CDF中,有22+(2-x)2=(2+x)2,
∴x=![]() ,
,
∴EF=![]() ∴,故B错误,
∴,故B错误,
∵PA∥CH,
∴∠CEP=∠ECH=∠BCH,
∴cos∠CEP=cos∠BCH=![]() =
=![]() ,故C错误.
,故C错误.
∵HF=![]() ,EF=
,EF=![]() ,FC=
,FC=![]()
∴HF2=EF·FC,故D正确,
故选:D.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目