题目内容
如图,在ΔABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心
在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是____________
在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是____________

1
试题分析:连接OA,OQ,OD,设该圆半径为R,则有

在直角三角形
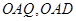 中,OQ=OD,OA是公共边,所以
中,OQ=OD,OA是公共边,所以 ,所以AQ=AD,
,所以AQ=AD,已知在三角形ABC中,角C等于90,AC=8,AB=10,由勾股定理知
BC=6,而且CP=AC-AP=6,可得三角形BCP是等腰直角三角形,所以
 ,因为
,因为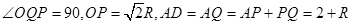



点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 是⊙
是⊙ 的直径,
的直径,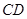 是⊙
是⊙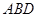 =56°,则∠
=56°,则∠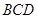 = 度.
= 度.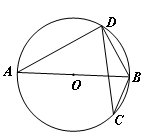
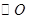 的半径为3,圆心
的半径为3,圆心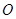 到直线
到直线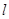 的距离为5,则直线
的距离为5,则直线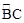 的长为 cm.
的长为 cm.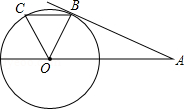
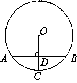
 上一点,则∠D= °.
上一点,则∠D= °. 
 =
= ,点E为OD上任意一点(不与O、D重合).求证:AE=BE.
,点E为OD上任意一点(不与O、D重合).求证:AE=BE.
