题目内容
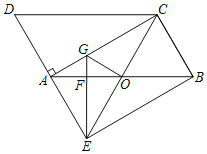
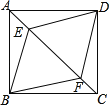
【题目】如图，正方形ABCD中，E、F是对角线AC上两点，连接BE、BF、DE、DF，则添加下列条件①∠ABE＝∠CBF；②AE＝CF；③AB＝AF；④BE＝BF．可以判定四边形BEDF是菱形的条件有（ ）
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据正方形的四条边都相等，对角线互相垂直平分且每一条对角线平分一组对角的性质，再加上各选项的条件，对各选项分析判断后即可得出正确选项的个数
解：如图，连接BD，交AC于点O，
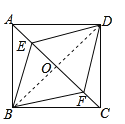
在正方形ABCD中，AB=BC，∠BAC=∠ACB，AC⊥BD，AO=CO，BO=DO，
①在△ABE与△BCF中，
，
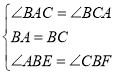∴△ABE≌△BCF（ASA），
∴BE=BF，
∵AC⊥BD，
∴OE=OF，
所以四边形BEDF是菱形，故①选项正确；
②在正方形ABCD中，AC=BD，
∴OA=OB=OC=OD，
∵AE=CF，
∴OE=OF，又EF⊥BD，BO=OD，
∴四边形BEDF是菱形，故②选项正确；
③AB=AF，不能推出四边形BEDF其它边的关系，故不能判定是菱形，本选项错误；
④BE=BF，同①的后半部分证明，故④选项正确．
所以①②④共3个可以判定四边形BEDF是菱形．
故选：C．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
