题目内容
【题目】全善学校为了提高学生综合能力,培养学生兴趣,决定开设以下精品校本课程:A. 创新与实践,B. 数学之美,C.英美文学鉴赏,D. 小小外交家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
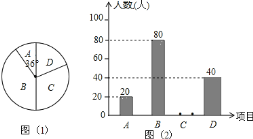
(1)这次被调查的学生共有______人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,有三男一女四名同学表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好选到一男一女两位同学的概率(用树状图或列表法解答).
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)由A是36°,A的人数为20人,即可求得这次被调查的学生总人数;
(2)由(1),可求得C的人数,即可将条形统计图(2)补充完整;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好同时选中甲、乙两位同学的情况,然后利用概率公式求解即可求得答案.
(1)∵A是36°,
∴A占36°÷360=10%,
∵A的人数为20人,
∴这次被调查的学生共有:20÷10%=200(人),
故答案为:200;
(2)如图,C有:200-20-80-40=60(人),

(3)画树状图得:

∵共有12种等可能的结果,恰好同时选中甲、乙两位同学的有2种情况,
∴恰好同时选中甲、乙两位同学的概率为:![]() .
.

 阅读快车系列答案
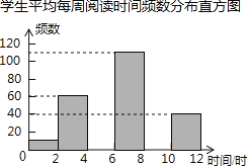
阅读快车系列答案【题目】为引导学生广泛阅读古今文学名著,某校开展了读书活动.学生会随机调查了部分学生平均每周阅读时间的情况,整理并绘制了如下的统计图表:
学生平均每周阅读时间频数分布表
平均每周阅读时间x(时) | 频数 | 频率 |
0≤x<2 | 10 | 0.025 |
2≤x<4 | 60 | 0.150 |
4≤x<6 | a | 0.200 |
6≤x<8 | 110 | b |
8≤x<10 | 100 | 0.250 |
10≤x≤12 | 40 | 0.100 |
合计 | 400 | 1.000 |
请根据以上信息,解答下列问题;
(1)在频数分布表中,a=______,b=______;
(2)补全频数分布直方图;
(3)如果该校有1600名学生,请你估计该校平均每周阅读时间不少于6小时的学生大约有多少人?