题目内容
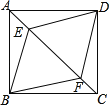
【题目】如图，点 B、D、E 在一条直线上，BE 与 AC 相交于点 F，
，连接 EC．
（1）求证：△ABD∽△ACE；
（2）若∠BAD=21°，求∠EBC 的度数．
【答案】(1)证明见解析;⑵∠EBC =21°.
【解析】
（1）根据相似三角形的性质定理得到∠BAC=∠DAE，结合图形，证明即可；
（2）根据相似三角形的性质即可得到结论．
（1）∵
=
=
，∴△ABC～△ADE；
∴∠BAC=∠DAE，∴∠BAC﹣∠DAF=∠DAE﹣∠DAF，即∠BAD=∠CAE．
∵=，∴△ABD∽△ACE．
（2）∵△ABC～△ADE，∴∠ABC=∠ADE．
∵∠ABC=∠ABE+∠EBC，∠ADE=∠ABE+∠BAD，∴∠EBC=∠BAD=21°．
练习册系列答案
相关题目
【题目】某班为准备半期考表彰的奖品，计划从友谊超市购买笔记本和水笔共40件．在获知某网店有 “双十一”促销活动后，决定从该网店购买这些奖品．已知笔记本和水笔在这两家商店的零售价分别如下表，且在友谊超市购买这些奖品需花费125元．
品名 商店 | 笔记本 （元/件） | 水笔 （元/件） |
友谊超市 | 5 | 2 |
网店 | 4 |
|
（1）班级购买的笔记本和水笔各多少件？
（2）求从网店购买这些奖品可节省多少元？
