题目内容
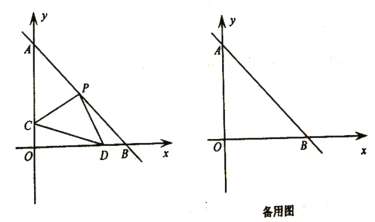
【题目】如图,直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.
轴相交于点B.
(1)求A、B两点的坐标;
(2)求△AOB的面积;
(3)若点P是![]() 轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
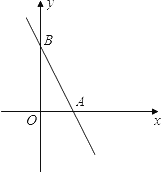
【答案】(1)A(2,0),B(4,0);(2)面积为4;(3)(![]() ,0),(
,0),(![]() ,0),(-2,0),(-4,0)
,0),(-2,0),(-4,0)
【解析】
(1)把x=0,y=0分别代入函数解析式,即可求得相应的y、x的值,则易得点A、B的坐标;
(2)根据三角形面积计算公式求解即可;
(3)根据等腰三角形的判定,分两种情况讨论即可求得.
(1)∵当y=0时,x=2;当x=0时,y=4,
∴A(2,0),B(0,4);
(2)S△AOB=![]() ×2×4=4;
×2×4=4;
(3)∵A(2,0),B(0,4).
∴AB=![]() ,
,
当AB为腰长时,P的坐标为(![]() ,0),(
,0),(![]() ,0)或(-2,0),
,0)或(-2,0),
当AB为底时,则AP=BP,设P(x,0)
则AP=2-x,
故在Rt△BOP中,
BO 2+OP2=BP 2,
即42+x2=(2-x)2,
解得:x=-3,
故P点坐标为(-3,0).
故P的坐标为:(-3,0)或(-2,0)或(![]() ,0)或(
,0)或(![]() ,0);
,0);

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目