题目内容
如图,已知直线y=x与抛物线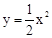 交于A、B两点.
交于A、B两点.
(1)求交点A、B的坐标;
(2)记一次函数y=x的函数值为y1,二次函数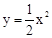 的函数值为y2.若y1>y2,求x的取值范围;
的函数值为y2.若y1>y2,求x的取值范围;
(3)在该抛物线上存在几个点,使得每个点与AB构成的三角形为等腰三角形?并求出不少于3个满足条件的点P的坐标.
(1)A(0,0),B(2,2)。
(2)0<x<2。
(3)符号条件的点P有4个,
其中P1( ,
, ),P2(
),P2( ,
, ),P3(﹣2,2)。
),P3(﹣2,2)。
解析试题分析:(1)根据题意可以列出关于x、y的方程组 ,通过解方程组可以求得点A、B的坐标。
,通过解方程组可以求得点A、B的坐标。
(2)根据函数图象可以直接回答问题;
(3)需要分类讨论:以AB为腰和以AB为底的等腰三角形。
解:(1)如图,∵直线y=x与抛物线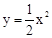 交于A、B两点,
交于A、B两点,
∴ ,解得,
,解得, 或
或 。
。
∴A(0,0),B(2,2)。
(2)由(1)知,A(0,0),B(2,2).
∵一次函数y=x的函数值为y1,二次函数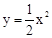 的函数值为y2,
的函数值为y2,
∴当y1>y2时,根据图象可知x的取值范围是:0<x<2。
(3)该抛物线上存在4个点,使得每个点与AB构成的三角形为等腰三角形。理由如下:
∵A(0,0),B(2,2),∴B= 。
。
根据题意,可设P(x, ),
),
①当PA=PB时,点P是线段AB的中垂线与抛物线的交点,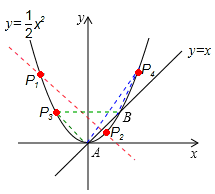
易求线段AB的中垂线的解析式为y=﹣x+2,
则 ,
,
解得, ,
, 。
。
∴P1( ,
, ),P2(
),P2( ,
, )。
)。
②当PA=AB时,根据抛物线的对称性知,点P与点B关于y轴对称,即P3(﹣2,2)。
③当AB=PB时,点P4的位置如图所示。
综上所述,符号条件的点P有4个,
其中P1( ,
, ),P2(
),P2( ,
, ),P3(﹣2,2)。
),P3(﹣2,2)。

练习册系列答案
相关题目


 (a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
(a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.

 经过点A(
经过点A( ,0)和点B(1,
,0)和点B(1, ),与x轴的另一个交点为C.
),与x轴的另一个交点为C. ∠MFO时,请直接写出线段BM的长.
∠MFO时,请直接写出线段BM的长.
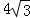 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(t≥0).
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(t≥0).
 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG﹣GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG﹣GD以每秒 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA﹣AC于P点,则是否存在t的值,使得PC⊥EQ,若存在,请求出t的值;若不存在,请说明理由.
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA﹣AC于P点,则是否存在t的值,使得PC⊥EQ,若存在,请求出t的值;若不存在,请说明理由. 的顶点A(2,0),与y轴的交点为B(0,-1).
的顶点A(2,0),与y轴的交点为B(0,-1).
 (x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )