题目内容
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为 ,点E的坐标为 ;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
(3)如图,若点E的纵坐标为-1,抛物线 (a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
(a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
解:(1)点B的坐标为(3,4),点E的坐标为(0,1)。
(2)点E能恰好落在x轴上。理由如下:
∵四边形OABC为矩形,∴BC=OA=4,∠AOC=∠DCE=90°。
由折叠的性质可得:DE=BD=OA-CD=4-1=3,AE=AB=OC=m。
如图1,假设点E恰好落在x轴上,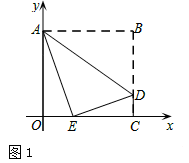
在Rt△CDE中,由勾股定理可得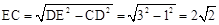 ,
,
则有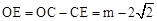 。
。
在Rt△AOE中,OA2+OE2=AE2,
即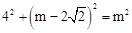 ,解得
,解得 。
。
(3)如图2,过点E作EF⊥AB于F,EF分别与AD、OC交于点G、H,过点D作DP⊥EF于点P,则EP=PH+EH=DC+EH=2,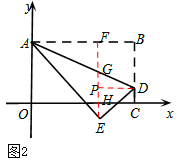
在Rt△PDE中,由勾股定理可得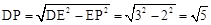 ,
,
∴BF=DP=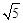 。
。
在Rt△AEF中,AF=AB?BF=m?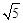 ,EF=5,AE=m,
,EF=5,AE=m,
∵AF2+EF2=AE2,即 ,解得m=3
,解得m=3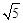 。
。
∴AB=3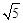 ,AF=2
,AF=2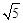 ,E(2
,E(2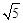 ,-1)。
,-1)。
∵∠AFG=∠ABD=90°,∠FAG=∠BAD,∴△AFG∽△ABD。
∴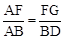 ,即
,即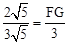 ,解得FG=2。∴EG=EF-FG=3。∴点G的纵坐标为2。
,解得FG=2。∴EG=EF-FG=3。∴点G的纵坐标为2。
∵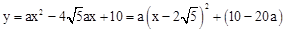 ,
,
∴此抛物线的顶点必在直线x=2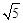 上。
上。
又∵抛物线 的顶点落在△ADE的内部,
的顶点落在△ADE的内部,
∴此抛物线的顶点必在EG上。
∴-1<10-20a<2,解得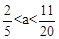 。
。
∴a的取值范围为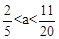 。
。
解析试题分析:(1)根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标。
(2)由折叠的性质求得线段DE和AE的长,然后利用勾股定理得到有关m的方程,求得m的值即可。
(3)过点E作EF⊥AB于F,EF分别与 AD、OC交于点G、H,过点D作DP⊥EF于点P,首先利用勾股定理求得线段DP的长,从而求得线段BF的长,再利用△AFG∽△ABD得到比例线段求得线段FG的长,最后求得a的取值范围。

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案若反比例函数y= 的图象经过点(m,3m),其中m≠0,则此反比例函数的图象在
的图象经过点(m,3m),其中m≠0,则此反比例函数的图象在
| A.第一、二象限 | B.第一、三象限 |
| C.第二、四象限 | D.第三、四象限 |

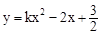 (
( 是常数)
是常数) 轴只有一个交点,求
轴只有一个交点,求 在某反比例函数的图像上,要使该反比例函数和二次函数
在某反比例函数的图像上,要使该反比例函数和二次函数 随
随 两点,且
两点,且 ,
, ,在
,在

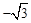 ),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).

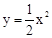 交于A、B两点.
交于A、B两点.