题目内容
如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
解:(1)∵点A(﹣1,0)在抛物线y=﹣(x﹣1)2+c上,
∴0=﹣(﹣1﹣1)2+c,解得c=4。
∴抛物线解析式为:y=﹣(x﹣1)2+4。
令x=0,得y=3,∴C(0,3);
令y=0,得x=﹣1或x=3,∴B(3,0)。
(2)△CDB为直角三角形。理由如下:
由抛物线解析式,得顶点D的坐标为(1,4)。
如答图1所示,过点D作DM⊥x轴于点M,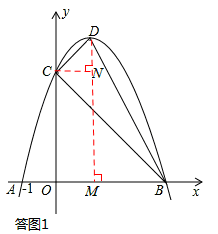
则OM=1,DM=4,BM=OB﹣OM=2。
过点C作CN⊥DM于点N,
则CN=1,DN=DM﹣MN=DM﹣OC=1。
在Rt△OBC中,由勾股定理得: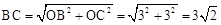 ;
;
在Rt△CND中,由勾股定理得: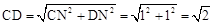 ;
;
在Rt△BMD中,由勾股定理得: 。
。
∵BC2+CD2=BD2,∴根据勾股定理的逆定理,得△CDB为直角三角形。
(3)设直线BC的解析式为y=kx+b,
∵B(3,0),C(0,3),∴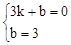 ,解得
,解得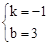 。
。
∴直线BC的解析式为y=﹣x+3。
∵直线QE是直线BC向右平移t个单位得到,
∴直线QE的解析式为:y=﹣(x﹣t)+3=﹣x+3+t。
设直线BD的解析式为y=mx+m,
∵B(3,0),D(1,4),∴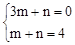 ,解得:
,解得: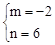 。
。
∴直线BD的解析式为y=﹣2x+6。
连接CQ并延长,射线CQ交BD于点G,则G( ,3)。
,3)。
在△COB向右平移的过程中:
①当0<t≤ 时,如答图2所示:
时,如答图2所示: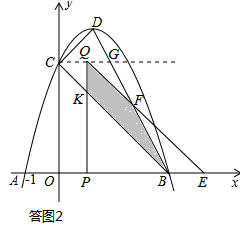
设PQ与BC交于点K,可得QK=CQ=t,PB=PK=3﹣t.
设QE与BD的交点为F,
则: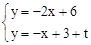 ,解得
,解得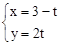 ,∴F(3﹣t,2t)。
,∴F(3﹣t,2t)。
∴S=S△QPE﹣S△PBK﹣S△FBE
= PE•PQ﹣
PE•PQ﹣ PB•PK﹣
PB•PK﹣ BE•yF
BE•yF
= ×3×3﹣
×3×3﹣ (3﹣t)2﹣
(3﹣t)2﹣ t•2t=
t•2t=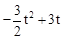 。
。
②当 <t<3时,如答图3所示,
<t<3时,如答图3所示,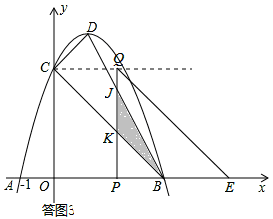
设PQ分别与BC、BD交于点K、点J,
∵CQ=t,∴KQ=t,PK=PB=3﹣t。
直线BD解析式为y=﹣2x+6,令x=t,得y=6﹣2t。∴J(t,6﹣2t)。
∴S=S△PBJ﹣S△PBK= PB•PJ﹣
PB•PJ﹣ PB•PK=
PB•PK= (3﹣t)(6﹣2t)﹣
(3﹣t)(6﹣2t)﹣ (3﹣t)2=
(3﹣t)2= t2﹣3t+
t2﹣3t+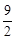 。
。
综上所述,S与t的函数关系式为:S=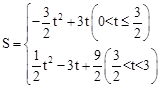 。
。
解析试题分析:(1)首先用待定系数法求出抛物线的解析式,然后进一步确定点B,C的坐标。
(2)分别求出△CDB三边的长度,利用勾股定理的逆定理判定△CDB为直角三角形。
(3)△COB沿x轴向右平移过程中,分两个阶段:
①当0<t≤ 时,如答图2所示,此时重叠部分为一个四边形;
时,如答图2所示,此时重叠部分为一个四边形;
②当 <t<3时,如答图3所示,此时重叠部分为一个三角形。
<t<3时,如答图3所示,此时重叠部分为一个三角形。

 的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.



 .
.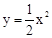 交于A、B两点.
交于A、B两点.

 经过点A、B、C.
经过点A、B、C.
 上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )