��Ŀ����
��ͼ����֪����ABCΪ�߳���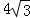 �ĵȱ������Σ��ı���DEFGΪ�߳���6�������Σ��ֽ��ȱߡ�ABC��������DEFG����ͼ1�ķ�ʽ�ڷţ�ʹ��C���E�غϣ���B��C��E����F��ͬһ��ֱ���ϣ���ABC��ͼ1��λ�ó�������ÿ��1����λ���ȵ��ٶ���EF�������������˶�������C���F�غ�ʱ��ͣ�˶������ABC���˶�ʱ��Ϊt�루t��0����
�ĵȱ������Σ��ı���DEFGΪ�߳���6�������Σ��ֽ��ȱߡ�ABC��������DEFG����ͼ1�ķ�ʽ�ڷţ�ʹ��C���E�غϣ���B��C��E����F��ͬһ��ֱ���ϣ���ABC��ͼ1��λ�ó�������ÿ��1����λ���ȵ��ٶ���EF�������������˶�������C���F�غ�ʱ��ͣ�˶������ABC���˶�ʱ��Ϊt�루t��0����
��1���������˶������У���ȱߡ�ABC��������DEFG�ص����ֵ����ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ��
��2����ͼ2������A���D�غ�ʱ������ABE�Ľ�ƽ����BM��AE��M�㣬����ABM�Ƶ�A��ʱ����ת��ʹ��AB���AC�غϣ��õ���ACN�����߶�AG���Ƿ����H�㣬ʹ�á�ANHΪ���������Σ�������ڣ�������߶�EH�ij��ȣ��������ڣ���˵�����ɣ�
��3����ͼ3�����ı���DEFGΪ�߳�Ϊ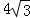 �������Σ���ABC���ƶ��ٶ�Ϊÿ��
�������Σ���ABC���ƶ��ٶ�Ϊÿ�� ����λ���ȣ������������ֲ��䣮��ABC��ʼ�ƶ���ͬʱ��Q���F�㿪ʼ��������FG��GD��ÿ��
����λ���ȣ������������ֲ��䣮��ABC��ʼ�ƶ���ͬʱ��Q���F�㿪ʼ��������FG��GD��ÿ�� ����λ���ȿ�ʼ�ƶ�����ABCֹͣ�˶�ʱ��Q��Ҳֹͣ�˶��������˶������У�DE������BA��AC��P�㣬���Ƿ����t��ֵ��ʹ��PC��EQ�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
����λ���ȿ�ʼ�ƶ�����ABCֹͣ�˶�ʱ��Q��Ҳֹͣ�˶��������˶������У�DE������BA��AC��P�㣬���Ƿ����t��ֵ��ʹ��PC��EQ�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��1��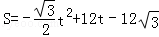
��2��������
��3��������
���������������1��������������������ε������ʽ���Ա�ʾ��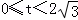 ʱ�ص����ֵ��������
ʱ�ص����ֵ��������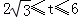 ʱ��S��ABC��
ʱ��S��ABC�� �Ϳ�������ص����ֵ������
�Ϳ�������ص����ֵ������
��2������A���D�غ�ʱ��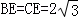 �����������������AN��ֵ������������������EH��ֵ����AN=AH=4ʱ����AN=NH=4ʱ����ʱH�����߶�AG���ӳ����ϣ���AH=NHʱ����ʱH��Ϊ�߶�AG���д�����AG�Ľ��㣬�Ӷ���������𰸣�
�����������������AN��ֵ������������������EH��ֵ����AN=AH=4ʱ����AN=NH=4ʱ����ʱH�����߶�AG���ӳ����ϣ���AH=NHʱ����ʱH��Ϊ�߶�AG���д�����AG�Ľ��㣬�Ӷ���������𰸣�
��3�����˶��е�0��t��2ʱ����ͼ2����PEC�ס�EFQ���������tֵ����2��t��4ʱ����ͼ3����PEC�ס�QDF���������tֵ��
�⣺��1����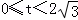 ʱ��
ʱ��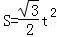
�� ʱ��
ʱ��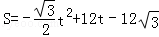 ��
��
��2������A���D�غ�ʱ��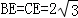 ��
��
��BMƽ�֡�ABE��
��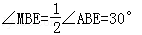
��ME=2��
�ߡ�ABM=��BAM��
��AM=BM=4��
�ߡ�ABM�ա�ACN��
���CAN=30�㣬AN=4
��AN=AH=4ʱ��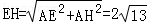 ��
��
��AN=NH=4ʱ����ʱH�����߶�AG���ӳ����ϣ�����ȥ��
��AH=NHʱ����ʱH��Ϊ�߶�AG���д�����AG�Ľ��㣬��ͼ1��
��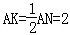 ��
��
��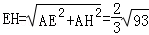 ��
��
��3����0��t��2ʱ����ͼ2����PEC�ס�EFQ��
�� ��
��
��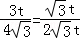 ��
��
��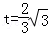 ��
��
��2��t��4ʱ����ͼ3����PEC�ס�QDE��
��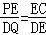 ��
��
��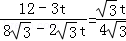 ��
��
��
�� ��
��
��t1=4��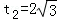 ��
��
���������⿼���������Ľ���ʽ�������ε����ʣ�ȫ�������ε��ж������ʣ����������ε����ʣ��ȱ������ε����ʣ����ɶ��������ã�

������������y= ��ͼ����(m��3m)������m��0����˷�����������ͼ����
��ͼ����(m��3m)������m��0����˷�����������ͼ����
| A����һ�������� | B����һ�������� |
| C���ڶ��������� | D�������������� |
������ͼ��ʾ������㺯��ֵ���������x��ֵΪ ��������ĺ���ֵΪ (����)
��������ĺ���ֵΪ (����)
A��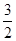 | B�� | C�� | D�� |
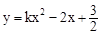 ��
�� �dz�����
�dz����� ��ֻ��һ�����㣬��
��ֻ��һ�����㣬�� ��ij������������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ���
��ij������������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ��� ��
�� ���㣬��
���㣬�� ��
�� ����
����
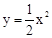 ����A��B���㣮
����A��B���㣮

 ��
�� ��
�� ������A��B��C��
������A��B��C��