Question

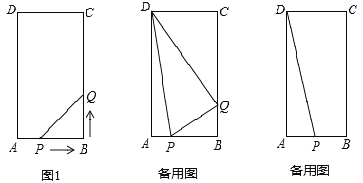
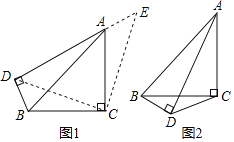
【题目】如图，是具有公共边AB的两个直角三角形，其中，AC=BC，∠ACB=∠ADB=90°．

(1)如图1，若延长DA到点E，使AE=BD，连接CD，CE．

①求证：CD=CE，CD⊥CE；

②求证：AD+BD=CD；

(2)若△ABC与△ABD位置如图2所示，请直接写出线段AD，BD，CD的数量关系．

Answer 1

【答案】(1)①证明见解析；②证明见解析；(2)AD-BD=CD.

【解析】

(1)①根据四边形的内角和得到∠DAC+∠DBC=180°，推出∠DBC=∠EAC，根据全等三角形的性质得到CD=CE，∠BCD=∠ACE，求得∠DCE=90°，根据垂直的定义得到结论；

②由已知条件得到△CDE是等腰直角三角形，求得DE=CD，根据线段的和差即可得到结论；

(2)如图2，在AD上截取AE=BD，连接CE，根据等腰直角三角形的性质得到∠BAC=∠ABC=45°，求得∠CBD=∠CAE，根据全等三角形的性质得到CD=CE，∠BCD=∠ACE，求得∠DCE=90°，根据线段的和差即可得到结论．

(1)证明：①在四边形ADBC中，∠DAC+∠DBC+∠ADB+∠ACB=360°，

∵∠ADB+∠ACB=180°，

∴∠DAC+∠DBC=180°，

∵∠EAC+∠DAC=180°，

∴∠DBC=∠EAC，

∵BD=AE，BC=AC，

∴△BCD≌△ACE(SAS)，

∴CD=CE，∠BCD=∠ACE，

∵∠BCD+∠DCA=90°，

∴∠ACE+∠DCA=90°，

∴∠DCE=90°，

∴CD⊥CE；

②∵CD=CE，CD⊥CE，

∴△CDE是等腰直角三角形，

∴DE=CD，

∵DE=AD+AE，AE=BD，

∴DE=AD+BD，

∴AD+BD=CD；

(2)解：AD-BD=CD；

理由：如图2，在AD上截取AE=BD，连接CE，

∵AC=BC，∠ACB=90°，

∴∠BAC=∠ABC=45°，

∵∠ADB=90°，

∴∠CBD=90°-∠BAD-∠ABC=90°-∠BAD-45°=45°-∠BAD，

∵∠CAE=∠BAC-∠BAD=45°-∠BAD，

∴∠CBD=∠CAE，∵BD=AE，BC=AC，

∴△CBD≌△CAE(SAS)，

∴CD=CE，∠BCD=∠ACE，

∵∠ACE+∠BCE=∠ACB=90°，

∴∠BCD+∠BCE=90°，

即∠DCE=90°，

∴DE===CD，

∵DE=AD-AE=AD-BD，

∴AD-BD=CD．