题目内容
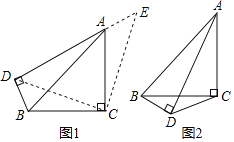
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
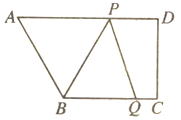
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
【答案】(1)s=96﹣6t (2)![]() 或
或![]()
【解析】
(1)点P作PM⊥BC,垂足为M,则四边形PDCM为矩形,根据三角形的面积公式就可以利用t表示,就得到S与t之间的函数关系式;
(2)以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ,②若BP=BQ,③若PB=PQ.
在Rt△PMQ中根据勾股定理,就得到一个关于t的方程,就可以求出t.
解:(1)过点P作PM⊥BC于M,则四边形PDCM为矩形.
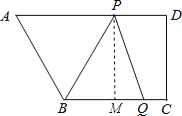
∴PM=DC=12,
∵QB=16﹣t,
∴S=![]() QBPM=
QBPM=![]() (16﹣t)×12=96﹣6t
(16﹣t)×12=96﹣6t
(2)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,
由PQ2=BQ2得t2+122=(16﹣t)2,解得t=![]() ;
;
②若BP=BQ,在Rt△PMB中,PB2=(16﹣2t)2+122,由PB2=BQ2得(16﹣2t)2+122=(16﹣t)2,即3t2﹣32t+144=0,
此时,△=(﹣32)2﹣4×3×144=﹣704<0,所以此方程无解,
∴BP≠BQ.
③若PB=PQ,由PB2=PQ2得t2+122=(16﹣2t)2+122得t1=![]() ,t2=16(不合题意,舍去).
,t2=16(不合题意,舍去).
综上所述,当t=![]() 或t=
或t=![]() 时,以B,P,Q三点为顶点的三角形是等腰三角形.
时,以B,P,Q三点为顶点的三角形是等腰三角形.

 初中暑期衔接系列答案
初中暑期衔接系列答案