题目内容
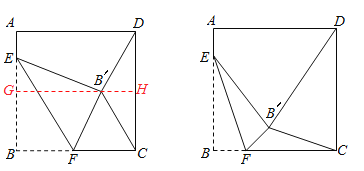
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处,若△CDB′恰为等腰三角形,则DB′的长为 .

【答案】16或4![]() .
.
【解析】
试题(1)当B′D=B′C时,过B′点作GH∥AD,则∠B′GE=90°,当B′C=B′D时,AG=DH=![]() DC=8,由AE=3,AB=16,得BE=13.由翻折的性质,得B′E=BE=13,∴EG=AG﹣AE=8﹣3=5,∴B′G=
DC=8,由AE=3,AB=16,得BE=13.由翻折的性质,得B′E=BE=13,∴EG=AG﹣AE=8﹣3=5,∴B′G=![]() =
=![]() =12,∴B′H=GH﹣B′G=16﹣12=4,∴DB′=
=12,∴B′H=GH﹣B′G=16﹣12=4,∴DB′=![]() =
=![]() =
=![]() ;
;
(2)当DB′=CD时,则DB′=16(易知点F在BC上且不与点C、B重合);
(3)当CB′=CD时,∵EB=EB′,CB=CB′,∴点E、C在BB′的垂直平分线上,∴EC垂直平分BB′,由折叠可知点F与点C重合,不符合题意,舍去.
综上所述,DB′的长为16或![]() .故答案为:16或
.故答案为:16或![]() .
.

练习册系列答案
相关题目