题目内容
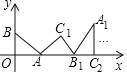
【题目】如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据三角形的滚动,可得出:每滚动3次为一个周期,点C1,C3,C5,…在第一象限,点C2,C4,C6,…在x轴上,由点A,B的坐标利用勾股定理可求出AB的长,进而可得出点C2的横坐标,同理可得出点C4,C6的横坐标,根据点的横坐标的变化可找出变化规律“点C2n的横坐标为2n×6(n为正整数)”,再代入2n=100即可求出结论.
解:根据题意,可知:每滚动3次为一个周期,点C1,C3,C5,…在第一象限,点C2,C4,C6,…在x轴上.
∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=![]() =5,
=5,
∴点C2的横坐标为4+5+3=12=2×6,
同理,可得出:点C4的横坐标为4×6,点C6的横坐标为6×6,…,
∴点C2n的横坐标为2n×6(n为正整数),
∴点C100的横坐标为100×6=600,
∴点C100的坐标为(600,0).
故选:B.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答年新型冠状病毒防治全国统一考试全国卷试卷满分![]() 分,社区管理员随机从有
分,社区管理员随机从有![]() 人的某小区抽取
人的某小区抽取![]() 名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
等级 | 成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
| |
根据上面提供的信息,回答下列问题: .
(1)统计表中的![]() ,
,![]() ,
,![]() ;
;
(2)请补全条形统计图;
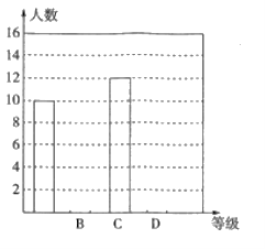
(3)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
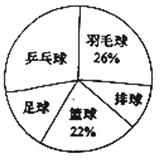
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.