题目内容
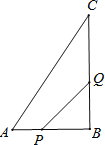
【题目】在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/秒的速度移动,同时,点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B.C两点后就停止移动,回答下列问题:
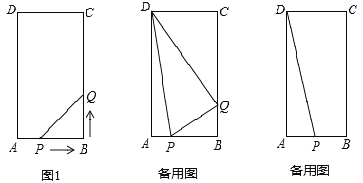
(1)运动开始后第几秒时, △PBQ的面积等于8![]() ?
?
(2)当t=![]() 时,试判断△DPQ的形状。
时,试判断△DPQ的形状。
(3)计算四边形DPBQ的面积,并探索一个与计算结果有关的结论。
【答案】(1)经过2秒或4秒,△PBQ的面积等于8cm2;(2)直角三角形;(3)36, 四边形DPBQ的面积是固定值36.
【解析】
(1)设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;
(2)表示出DP 2=146.25,PQ 2=29.25,DQ 2=117,进而得到PQ 2+DQ 2=DP 2,得出答案;
(3)根据表示出四边形面积,求出即可.
解:(1)设经过t秒,△PBQ的面积等于8cm2则:
BP=6-t,BQ=2t,
所以S△PBQ=![]() ×(6-t)×2t=8,即t2-6t+8=0,
×(6-t)×2t=8,即t2-6t+8=0,
可得:t=2或4,即经过2秒或4秒,△PBQ的面积等于8cm2.
(2)当t=1.5s时,
AP=1.5,BP=4.5,CQ=9,
∴DP 2=146.25,PQ 2=29.25,DQ 2=117,
∴PQ 2+DQ 2=DP 2,
∴△DPQ为直角三角形;
(3)SDPBQ=6×12-![]() t×12-
t×12-![]() ×6(12-2t),
×6(12-2t),
=72-36,
=36,
∴四边形DPBQ的面积是固定值36.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目