题目内容
如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y= (x>0) 的图象上,点C在反比例函数L2:y=
(x>0) 的图象上,点C在反比例函数L2:y=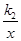 (x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为 .(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
(x>0) 的图象上(矩形ABCD夹在L1与L2之间).(1)若点A坐标为(1,1)时,则L1的解析式为 .(2)在(1)的条件下,若矩形ABCD是边长为1的正方形,求L2的解析式.(3)若k1=1,k2=6,且矩形ABCD的相邻两边分别为1和2,求符合条件的顶点C的坐标.
(1)y=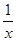 (x>0);(2)y=
(x>0);(2)y= 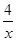 (x>0);符合题意的点C的坐标为(4,
(x>0);符合题意的点C的坐标为(4, )或(3,2)或(
)或(3,2)或( ,4)或(2,3).
,4)或(2,3).
解析试题分析:(1)点A(1,1)在反比例函数y=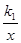 上,则将x=1,y=1代入反比例函数式中,等式一定成立,所以有k1=1.(2)根据题意,将点A向右平移1个单位,再向上平移1个单位,就得到点C,所以点C的坐标是(2,2),将点C(2,2)代入反比例函数y=
上,则将x=1,y=1代入反比例函数式中,等式一定成立,所以有k1=1.(2)根据题意,将点A向右平移1个单位,再向上平移1个单位,就得到点C,所以点C的坐标是(2,2),将点C(2,2)代入反比例函数y=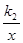 得k2=4.(3)设点A的横坐标是a,则纵坐标是
得k2=4.(3)设点A的横坐标是a,则纵坐标是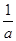 ,分两种情况讨论:当AB=1,AD=2时,此时,点C的坐标应为(a+1,
,分两种情况讨论:当AB=1,AD=2时,此时,点C的坐标应为(a+1, 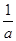 +2),代入直线L2的关系式中,即可求得点C的坐标;当AB=2,AD=1时,点C的坐标可表示为(a+2,
+2),代入直线L2的关系式中,即可求得点C的坐标;当AB=2,AD=1时,点C的坐标可表示为(a+2, 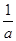 +1),代入直线L2的表达式中,就可求得点C的坐标.
+1),代入直线L2的表达式中,就可求得点C的坐标.
试题解析:(1)y=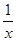 (x>0);(2)y=
(x>0);(2)y=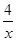 (x>0)
(x>0)
(3)①当AB=1,AD=2时,设A点坐标为(a,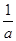 ),则C点坐标为(a+1,
),则C点坐标为(a+1, 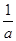 +2),
+2),
由已知有(a+1)(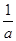 +2)=6,解得a=1或a=
+2)=6,解得a=1或a=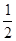
故此时符合条件的C点有( ,4)和(2,3)
,4)和(2,3)
②当AB=2,AD=1时,设A点坐标为(a,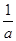 ),则C点坐标为(a+2,
),则C点坐标为(a+2,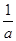 +1),
+1),
由已知有(a+2)(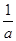 +1)=6,解得a=1或a=2
+1)=6,解得a=1或a=2
故此时符合条件的C点有(4, )和(3,2)
)和(3,2)
综上所述,符合题意的点C的坐标为(4, )或(3,2)或(
)或(3,2)或( ,4)或(2,3).
,4)或(2,3).
考点:反比例函数的图象

 经过点(2,3),如果A(a1,b1),B(a2,b2)两点在该双曲线上,且a1<0<a2,那么b1 b2.
经过点(2,3),如果A(a1,b1),B(a2,b2)两点在该双曲线上,且a1<0<a2,那么b1 b2.
 (x>0)的图象经过点B,D,求k的值.
(x>0)的图象经过点B,D,求k的值. m,DC的长为
m,DC的长为 m.
m.
 的图像与一次函数
的图像与一次函数 的图像交于点A(m,2),点B(-2, n ),一次函数图像与y轴的交点为C.求△AOC的面积。
的图像交于点A(m,2),点B(-2, n ),一次函数图像与y轴的交点为C.求△AOC的面积。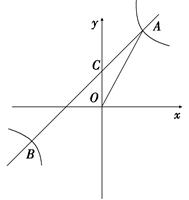
 的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
的图象在第二象限交与点C,如果点A为的坐标为(2,0),B是AC的中点.
 的图象交于点A,与x轴交于点B,AC⊥x轴于点C,
的图象交于点A,与x轴交于点B,AC⊥x轴于点C, ,AB=
,AB=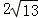 ,OB=OC.
,OB=OC.