题目内容
（1）先求解下列两题：
①如图①，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE，已知∠EDM=84°，求∠A的度数；
②如图②，在直角坐标系中，点A在y轴正半轴上，AC∥x轴，点B，C的横坐标都是3，且BC=2，点D在AC上，且横坐标为1，若反比例函数
(x＞0)的图象经过点B，D，求k的值．
（2）解题后，你发现以上两小题有什么共同点？请简单地写出．
（1）①21° ②k=3 （2）用已知的量通过关系去表达未知的量，使用转换的思维和方法．
解析解：（1）①∵AB=BC=CD=DE，
∴∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，
根据三角形的外角性质，∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，
又∵∠EDM=84°，
∴∠A+3∠A=84°，
解得，∠A=21°；
②∵点B在反比例函数y=
图象上，点B，C的横坐标都是3，
∴点B（3，
），
∵BC=2，
∴点C（3，+2），
∵AC∥x轴，点D在AC上，且横坐标为1，
∴A（1，+2），
∵点A也在反比例函数图象上，
∴+2=k，
解得，k=3；
（2）用已知的量通过关系去表达未知的量，使用转换的思维和方法．（开放题）
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
经过点（－1，2），那么k的值等于 .
(x>0)的图象交于点M，过M作MH⊥x，且tan∠AHO=
．
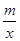的图象经过点C．
h）与排完水池中的水所用的时间t（h）之间的函数关系图象． 
，那么水池中的水要用多少小时排完？
在第一象限图象上的一点，已知△P1O A1为等边三角形，点A1的坐标为(2，0)．
(x＞0) 的图象上，点C在反比例函数L2：y＝
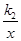(x＞0) 的图象上（矩形ABCD夹在L1与L2之间）．（1）若点A坐标为（1,1）时，则L1的解析式为 ．（2）在（1）的条件下，若矩形ABCD是边长为1的正方形，求L2的解析式．（3）若k1＝1，k2＝6，且矩形ABCD的相邻两边分别为1和2，求符合条件的顶点C的坐标．
，经过点P（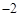
，
），点P关于
轴的对称点P′在反比例函数
（
）的图象上．
的图象经过点C．