题目内容
【题目】如图所示,BD为⊙O的直径,且BD=8,![]() 是圆周的
是圆周的![]() ,A为
,A为![]() 上任意一点,取AC=AB,交BD的延长线于C,连结OA,并作AE⊥BD于E,设AB=x,CD=y.
上任意一点,取AC=AB,交BD的延长线于C,连结OA,并作AE⊥BD于E,设AB=x,CD=y.
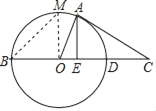
(1)写出y关于x的函数关系式;
(2)当x为何值时,CA是⊙O的切线?
(3)当CA与⊙O相切时,求tan∠OAE的值.
【答案】(1)y=![]() x2﹣8,(4
x2﹣8,(4![]() ≤x≤8);(2)当x=4
≤x≤8);(2)当x=4![]() 时,CA是⊙O的切线;(3)tan∠OAE=
时,CA是⊙O的切线;(3)tan∠OAE=![]() .
.
【解析】
(1)先证△AOB∽△BAC得![]() ,即
,即![]() 据此可得函数关系式,由A为MD上任意一点知BM≤AB≤BD,据此可得x的取值范围;
据此可得函数关系式,由A为MD上任意一点知BM≤AB≤BD,据此可得x的取值范围;
(2)由OA⊥CA时CA是⊙O的切线,据此知OC2=OA2+AC2,从而得出y2+8y=x2,结合函数关系式列方程组求解可得;
(3)由(2)知x=4![]() ,y=4时,CA是⊙O的切线,再求得OE=BE-BO=2,AE=
,y=4时,CA是⊙O的切线,再求得OE=BE-BO=2,AE= ![]() ,根据正切函数的定义计算可得.
,根据正切函数的定义计算可得.
(1)∵OA=OB,AB=AC,
∴∠ABO=∠BAO=∠C,
∴△AOB∽△BAC,
∴![]() ,即
,即![]() ,
,
∴y=![]() x2﹣8;
x2﹣8;
∵A为MD上任意一点,
∴BM≤AB≤BD,
∵BM=![]() ,BD=8,
,BD=8,
∴4![]() ≤x≤8,
≤x≤8,
∴y=![]() x2﹣8(4
x2﹣8(4![]() ≤x≤8);
≤x≤8);
(2)若OA⊥CA,则CA是⊙O的切线,
∴OC2=OA2+AC2,即(4+y)2=42+x2,即y2+8y=x2,
由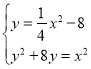 可得y=4,
可得y=4,
∴x=4![]() ,
,
∴当x=4![]() 时,CA是⊙O的切线;
时,CA是⊙O的切线;
(3)由(2)知x=4![]() ,y=4时,CA是⊙O的切线,
,y=4时,CA是⊙O的切线,
∴OE=BE﹣BO=![]() ×(8+4)﹣4=2,AE=
×(8+4)﹣4=2,AE=![]() ,
,
∴tan∠OAE=![]() .
.

练习册系列答案
相关题目